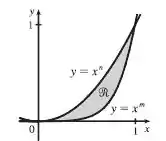
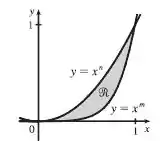
Seja a região que está entre as curvas e , , ondem e são inteiros com .
Esboce a região
Encontre as coordenadas do centroide de .
Tente encontrar valores de e tais que o centroide esteja fora de .
Passo 1
Esboçando , temos
Passo 2
Podemos calcular a área da seguinte maneira
Podemos então calcular as coordenadas do centroide
Passo 3
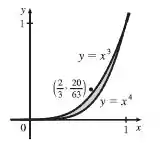
Tomando e , temos
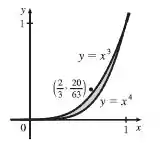
Como podemos ver, para tais valores se encontra fora da região.
Resposta