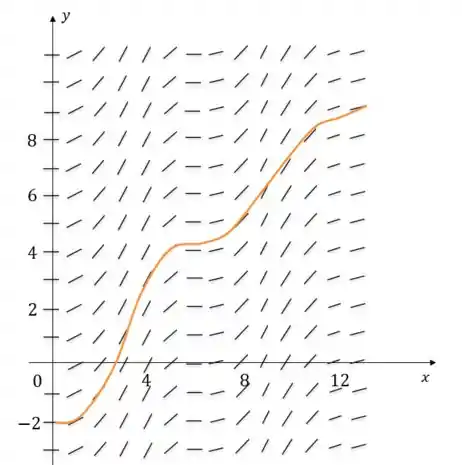
Um campo de direção é dado por uma função. Use-o para traçar a antiderivada que satisfaça .
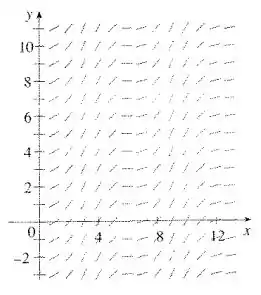
Passo 1
O campo de direções gerado por uma função indica o valor da função em cada ponto por meio de inclinações. Se é a antiderivada de então . Isso significa que representa a inclinação do gráfico de
Portanto, o campo de direções de f mostra as inclinações do gráfico de . Para traçar , basta seguir as inclinações a partir do ponto inicial do desenho.
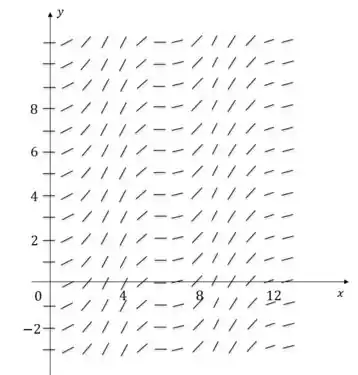
Passo 2
Partindo então do ponto dado e seguindo as linhas temos:
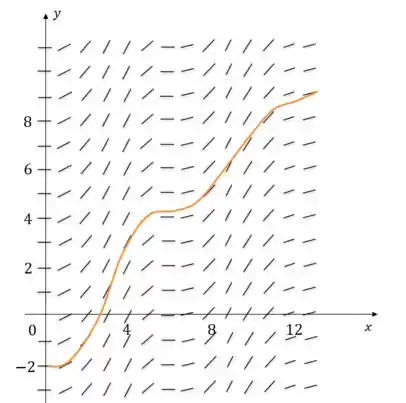
Resposta