Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.10 - Ex. 56
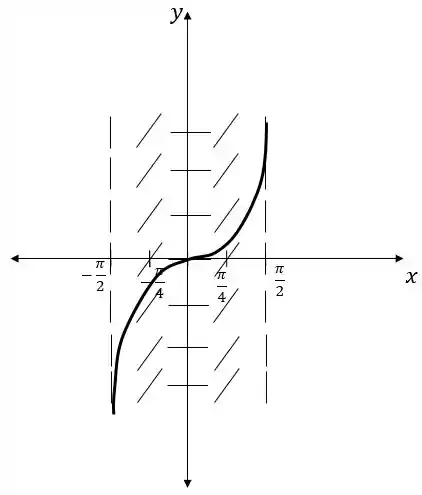
Use um campo de direção para fazer o gráfico da antiderivada que satisfaça .
Passo 1
Opa, tranquilo?
Vamos pensar aqui, quando nos é dado um gráfico de uma função derivada, podemos esboçar o gráfico da função que é a antiderivada a partir dele, ou seja fazer o gráfico da integral desta função;
Porém o exercício não nos deu um gráfico e sim uma função, o que temos que fazer então?
Vamos esboçar o gráfico para essa função e a partir disso chegar no gráfico de uma integral dessa função.
Passo 2
Vamos começar esboçando um campo de direções para a função no intervalo dado, e então usar o campo para traçar a antiderivada . O campo de direções é feito calculando o valor da função para alguns valores de e então fazendo pequenos segmentos de reta com a inclinação na reta vertical de .
Por exemplo, para , , então na reta vertical fazemos vários pequenos segmentos de inclinação (horizontais).
Passo 3
Vamos então calcular a função para alguns valores entre e :
Para
Para
Para
Para
E da mesma forma que o passo 1, vamos fazendo pequenas retas, nas direções dadas. Quando der , temos uma reta apontando para cima.
Assim conseguimos esboçar nosso campo de direções:
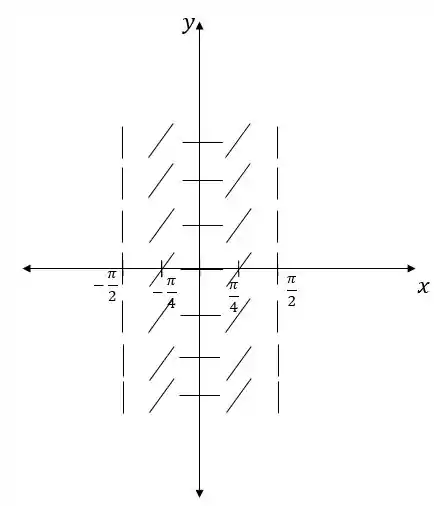
Passo 4
Agora usamos o campo de direções para traçar . Seria como se nossas retas fossem pequenos canos interligados e nosso lápis uma corrente de água passando por eles, escolha uma passagem e siga essa tubulação. Começamos a partir de , porque foi pedido no enunciado e então seguimos as direções dadas pelo campo. O gráfico então fica assim:
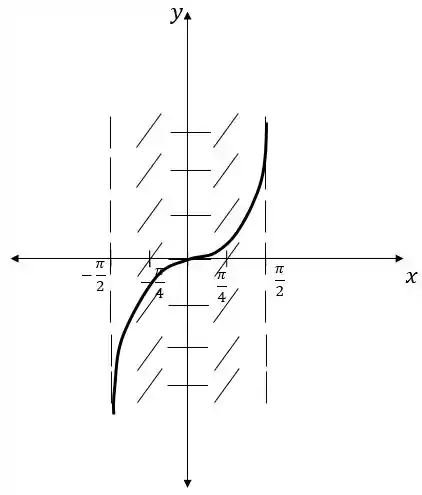
Resposta
