(a) Se , use os comandos discutidos no Exercício 9 para encontrar as somas esquerda e direita para e .
(b) Ilustre fazendo o gráfico dos retângulos da parte (a).
(c) Mostre que a área exata sob está entre e .
Passo 1
Veja o resolução do Exercício 9 para saber os comandos para avaliar as somas.
Passo 2
- Com , as somas esquerdas estão sob a forma:
- Pontos extremos esquerdos:
- Nós sabemos que desde que é uma função crescente em , e isso é verdade porque sua derivada é e é positiva nesse intervalo, todas as somas esquerdas são menores do que a área real, e todas as somas direitas são maiores. Desde que a soma esquerda com está entre e a soma direita, também com , está entre , nós concluímos que , logo, a área exata está entre e .
Então, especificamente,
As somas direitas estão sob a forma:
Então, especificamente:
Passo 3
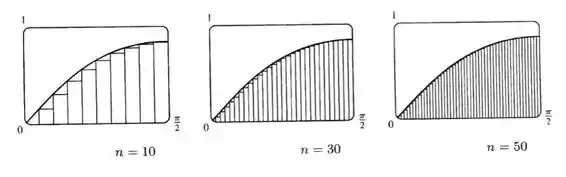
Pontos extremos direitos:
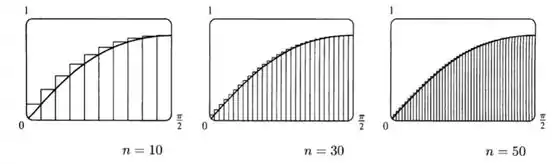
Passo 4
Resposta
Ei, a resposta está no passo a passo :)