Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.1 - Ex. 13

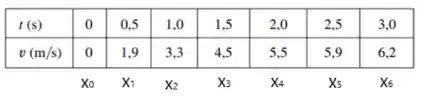
A velocidade de um corredor aumenta regularmente durante os três primeiros segundos de uma corrida. Sua velocidade em intervalos de meio segundo é dada em uma tabela. Ache as estimativas superior e inferior para a distância que ele percorreu durante esses três segundos.

Passo 1

Fala aí, galerinha! 😬

Nesse problema temos a velocidade de um corredor que aumenta regularmente durante os três primeiros segundos de uma corrida. Sua velocidade em intervalos de meio segundo é dada em uma tabela. A partir daí temos que achar as estimativas superior e inferior para a distância que ele percorreu durante esses três segundos.

Parece complicado? 😊

Como v é uma função crescente L 6 nos dará uma subestimativa e R 6 , uma superestimativa.

L pode ser calculado como

L = ∆ t x 0 + x 1 + x 2 + x 3 + … + x n - 1

Já R pode ser calculado como

R = ∆ t x 1 + x 2 + x 3 + x 4 + … + x n

Veja só! 😉

Passo 2

Calculando a subestimativa sabendo que ∆ t = 0,5 e que

L 6 = 0,5 0 + 1,9 + 3,3 + 4,5 + 5,5 + 5,9

L 6 = 10,55

Tranquilo até aqui? 😁

Passo 3

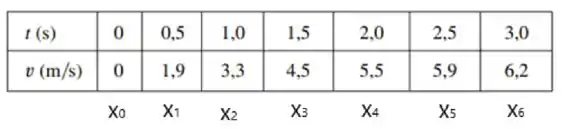
Calculando a superestimativa com ∆ t = 0,5 e

R 6 = 0,5 1,9 + 3,3 + 4,5 + 5,5 + 5,9 + 6,2

R 6 = 13,65

E aí! entendeu tudo? Responde Aí! 😁

Resposta

Subestimativa: 10,55

Superestimativa: 13,65

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja f x = 0 se x for um número racional qualquer e f x = 1 se x for um número irracional qualquer. Mostre que f não é integrável em 0,1 .
Seja f 0 = 0 e f x = 1 x se 0x ≤ 1 . Mostre que f não é integrável em 0,1 . [Sugestão: mostre que o primeiro termo na soma de Riemann, f x i * Δ x , pode ser tornado arbitrariamente grande.]
Encontre ∫ 1 2 x - 2 d x . Sugestão: Escolha x i * como a média geométrica de x i - 1 e x i (isto é, x i * = x i - 1 x i ) e use a identidade 1 m m + 1 = 1 m - 1 m + 1
Calcule o limite, reconhecendo primeiro a soma como uma soma de Riemann para uma função definida em 0,1 . lim n → ∞ ⁡ ∑ i = 1 n i 3 n 4
Calcule o limite, reconhecendo primeiro a soma como uma soma de Riemann para uma função definida em 0,1 . lim n → ∞ ⁡ 1 n 1 n + 2 n + 3 n + … + n n