Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.7 - Ex. 23
Use os dados do Exemplo 5 para achar a taxa média da mudança da temperatura em relação ao tempo.
das horas da noite às horas da noite.
das horas da noite às horas da noite.
das horas da noite às horas da noite.
Estime a taxa instantânea da variação de T em relação ao instante 8 horas medindo a inclinação de uma tangente.
Passo 1
Olá, meu esforçado estudante. Vou te ajudar a resolver mais uma atividade hoje.
Essa atividade pede que a gente use os dados do exemplo 5 e encontremos a taxa média da mudança da temperatura em relação ao tempo, sendo que o enunciado nos da alguns intervalos de tempo.
A primeira coisa para darmos início a nossa resolução é então pegar os dados do exemplo 5:
E para encontrarmos as taxas, estaremos sempre fazendo a divisão:
Em que é a variação de temperatura em graus celsius (°C) e é a variação do tempo em horas.
Passo 2
Sem mais enrolação, vamos começar colocando os valores de para os tempos que estão no enunciado.
Lembra que da noite é , da noite é , 10 da noite é e da noite é .
Fazendo a taxa, que é das horas da noite às horas da noite.
Substituindo os valores:
Fazendo a taxa, que é das horas da noite às horas da noite.
Substituindo os valores:
Fazendo a taxa, que é das horas da noite às horas da noite.
Substituindo os valores:
Passo 3
Letra b)
Colocamos os pontos no software GeoGebra, podemos ter uma noção maior do que iremos fazer aqui:
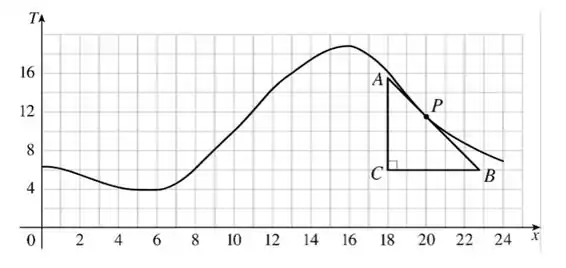
Temos então o ponto o ponto de tangencia, então vamos utilizar um triangulo para calcular a inclinação dessa reta tangente.
Na figura, estimamos que seja e seja . Você criar outro triangulo retângulo caso desejasse, criamos esse pois facilita nossos cálculos. Portanto, a inclinação é
às 20:00.
Porém, qual o sinal da taxa? A taxa é negativa, pois a tangente desse ângulo é um valor negativo, já que a reta é decrescente.
Resposta
taxa
taxa
taxa
Taxa instantânea igual a: