Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.4 - Ex. 6
Use os gráficos de e e suas retas em para encontrar
Passo 1
Fala aí! tudo certinho?
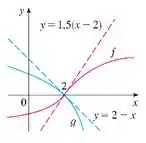
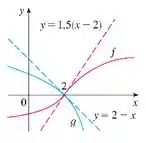
Nesse problema foi dado um gráfico com as funções em rosa, em azul e suas retas tangentes no ponto .
A partir daí, queremos descobrir qual é o valor do limite
Tem ideia de como fazemos isso?
Você pode pensar: “é fácil, é só ver quais são os valores de e em e substituir no limite”...
Vamos tentar?
Qual é o valor de em ? , não é? Certo... e agora, qual é o valor de em ? , correto?
Substituindo no limite, temos
Caímos em uma indeterminação!!
Quando isso acontece, uma ótima maneira de contornar esse problema é aplicando a regra de L’Hopital!
A regra de L’Hopital é aplicada quando temos que calcular o limite de uma função quando essa função tende a uma indeterminação ou ...
Na prática, a regra de L’Hopital consiste em derivar o numerador e o denominador separadamente e repetidamente até nos livrarmos da indeterminação.
Bora lá!
Passo 2
Podemos interpretar a derivada da função como a inclinação da reta tangente à função em um certo ponto.
As retas tangentes foram dadas no gráfico do problema
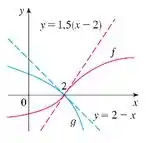
A reta tangente à é dada por
A reta tangente à é dada por
A inclinação de uma reta é dada pelo coeficiente que multiplica , lembra disso?
Então e .
Voltando para a regra de L’Hopital, como a inclinação da reta tangente é a derivada da função em um ponto, temos que
É isso! O que achou? Responde Aí!