Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.8 - Ex. 45

Use a definição de derivada para encontrar f ' x e f ' ' x . A seguir, trace f ,   f '   e   f ' ' em uma mesma tela e verifique se suas respostas são razoáveis.

f x = 1 + 4 x - x 2

Passo 1

Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Iremos utilizar a definição de derivadas e calcular a primeira e a segunda derivada da função. A pós isso iremos então encontrar os gráficos das derivadas.

Primeiramente, calculamos a primeira derivada, pela definição temos que

f ' x = lim h → 0 ⁡ f x + h - f x h

Passo 2

Então

f ' x = lim h → 0 ⁡ 1 + 4 x + h - x + h 2 - 1 - 4 x + x 2 h

Realizando os produtos:

= lim h → 0 ⁡ 1 + 4 x + 4 h - x 2 - 2 x h - h 2 - 1 - 4 x + x 2 h

Agora pós simplificação dos termos semelhantes:

= lim h → 0 ⁡ 4 h - 2 x h - h 2 h

Colocando h em evidencia:

= lim h → 0 ⁡ h 4 - 2 x - h h

= lim h → 0 ⁡ 4 - 2 x - h

= 4 - 2 x

f ' x = 4 - 2 x

Agora, podemos calcular a segunda derivada da seguinte maneira

f ' ' x = lim h → 0 ⁡ f ' x + h - f ' x h

Então

f ' ' x = lim h → 0 ⁡ 4 - 2 x + h - 4 + 2 x h

= lim h → 0 ⁡ 4 - 2 x - 2 h - 4 + 2 x h

= lim h → 0 ⁡ - 2 h h

= lim h → 0 ⁡ - 2

= - 2

f ' ' x = - 2

Passo 3

Esboçando os gráficos com ajuda do GeoGebra:

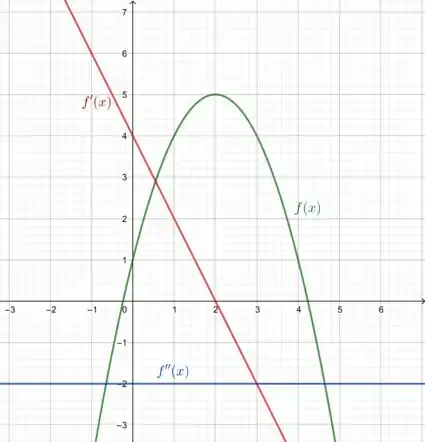
E veja que faz sentido, cada vez que derivamos um polinômio seu grau diminui em 1, então a segunda derivada de um polinômio do segundo grau é uma constante, assim como a primeira é uma reta.

Resposta

f ' x = 4 - 2 x

f ' ' x = - 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça o gráfico da funçãoExplique a forma do gráfico calculando o limite quando x → 0 + ou quando x → ∞ .Estime os valores máximo e mínimo e então use o cálculo para achar os valores exatos.Use o gráfi
Sef for a função considerada no Exemplo 3, use um sistema de computação algébrica para calcularf ' e então faça seu gráfico para confirmar que todos os valores máximos e mínimos são como dados no exem
Faça o gráfico da funçãoExplique a forma do gráfico calculando o limite quando x → 0 + ou quando x → ∞ .Estime os valores máximo e mínimo e então use o cálculo para achar os valores exatos.Use o gráfi
No Exemplo 4 consideramos um membro da família de funções f x = sen ⁡ ( x + sen ⁡ c x ) que ocorre na síntese de FM. Aqui investigamos a função com c = 3 . Comece o gráfico f com a janela retangular [
Use um sistema de computação algébrica para fazer o gráfico de f e encontrarf e f ' ' . Utilize os gráficos dessas derivadas para estimar os intervalos de crescimento e decrescimento, valores extremos