Use as derivadas primeira e segunda para mostrar que o gráfico de é sempre crescente e tem um ponto de inflexão na srcem.

Primeiro, vamos concordar que a função é definida para valores menores que 1, certo? Melhor dizendo, .

O gráfico abaixo demonstra como ela é uma função crescente!

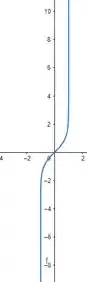
A derivada primeira dessa função é:

Já a derivada segunda, é:

Graficamente, temos:

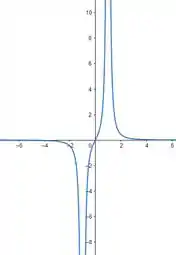
Essa derivada segunda, muda de sinal em , então existe um ponto de inflexão lá.

Prontinho!!!