Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 48
Use diferenciação implícita para mostrar que a função definida implicitamente por tem pontos críticos, sempre que . Use, então, o teste da derivada primeira ou segunda para classifica-los como máximos ou mínimos relativos.
Passo 1
Primeiro, vamos diferenciar a função dada:
Resolvendo , temos que:
Como dado pelo exercício
A função toda zera quando o numerador é igual a zero, e isso acontece em pontos de :
Generalizando até temos que :
Passo 2
Agora, vamos analisar o sinal graficamente, onde e são .
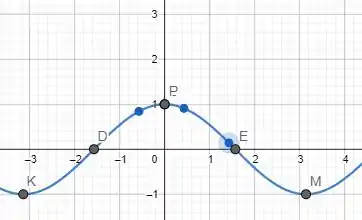
Analisando o gráfico, vemos que o ponto é um ponto de mínimo relativo, pois nesse intervalo ele decresce pela esquerda, no ponto , e posterioremente volta a aumentar. Ao passo que em é um ponto de máximo relativo.
Resposta
mínimo relativo.
máximo relativo.
Exercícios de Livros Relacionados
Encontre os valores de máximo e mínimo absoluto de f no intervalo dado f x = x - ln x , 1 2 , 2
Mostre que 5 é um número crítico da função g x = 2 + ( x - 5 ) 3 mas que g não tem um valor extremo local em 5 .
Entre 0 ° C e 30 ° C , o volume V (em centímetros cúbicos) de 1kg de água a uma temperatura T é aproximadamente dado pela fórmula V = 999,87 - 0,06426 T + 0,0085043 T 2 - 0,0000679 T 3 Encontre a temp
Um modelo para o preço médio norte-americano para o açúcar refinado entre, 1993 e 2003, é dado pela função S t =- 0,00003237 t 5 + 0 , 0009037 t 4 - 0,008956 t 3 + 0,03629 t 2 - 0,04458t + 0,4074 Onde
Um objeto com massa m é arrastado ao longo de um plano horizontal por uma força agindo ao longo de uma corda presa ao objeto. Se a corda faz um ângulo θ com o plano, então a intensidade da força é F =