Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 24

Use o Exercício 22 para encontrar o centroide da região triangular de vértices 0,0 ,   ( a , 0 ) e ( a , b ) , onde a > 0 e b > 0 .

Passo 1

Fala, galerinha! Tranquilo?

Nossa questão pede para encontrarmos o centroide do triângulo de vértices 0,0 ,   ( a , 0 ) e ( a , b ) , usando o exercício 22, que nos traz as seguintes equações para o centroide:

x - = 1 2 A ∮ C x 2   d y                     y - = - 1 2 A ∮ C y 2   d x

Aqui nossa curva C é o triângulo, então dividimos nossa figura em três segmentos de reta. Parametrizamos cada uma delas e somamos para ter o valor da integral de linha total.

Aqui a área A é a área do triângulo:

A = a b 2

Vamos lá!

Passo 2

Vamos esquematizar nosso triângulo:

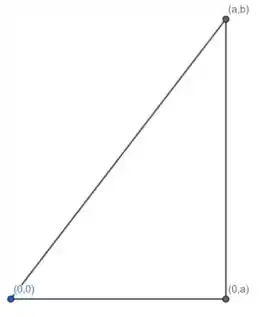
Podemos escrevê-lo como união das retas que ligam os pontos que são parametrizadas da forma:

  • Reta da base do triângulo:

    • r 1 t = t , 0 , 0 ≤ t ≤ a

  • Reta vertical:

    • r 2 t = a , t ,   0 ≤ t ≤ b

  • Reta diagonal:

r 3 t = a - a t , b - b t ,   0 ≤ t ≤ 1

A área do triângulo é:

A = a b 2

Substituindo nas equações do centroide:

x - = 1 a b ∮ C x 2   d y                     y - = - 1 a b ∮ C y 2   d x

Passo 3

Agora, vamos calcular as integrais. Calculando a componente x :

x - = 1 a b ∮ C x 2   d y = 1 a b ∫ C 1 x 2   d y + ∫ C 2 x 2   d y + ∫ C 3 x 2   d y

Calculando a primeira integral:

∫ C 1 x 2   d y = ∫ 0 a t 2 d d t ( 0 ) d t = 0

A segunda:

∫ C 2 x 2   d y = ∫ 0 b a 2 d d t t d t

Tirando a constante a 2 para fora:

= a 2 ∫ 0 b d t = a 2 b

A terceira integral:

∫ C 3 x 2   d y = ∫ 0 1 a - a t 2 d d t b - b t d t

Resolvendo a derivada do integrando:

= ∫ 0 1 a - a t 2 ( - b ) d t = a - a t 3 - 3 a - b 0 1

Aplicando os limites de integração:

= b 3 a - a 3 = - a 2 b 3

Somando as três integrais, para termos a integral do triângulo inteiro:

x - = 1 a b 0 + a 2 b - a 2 b 3 = 1 a b 2 a 2 b 3

Ficamos com:

x - = 2 a 3

Passo 4

Fazendo o mesmo procedimento para y :

y - = - 1 a b ∮ C y 2   d x = - 1 a b ∫ C 1 y 2   d x + ∫ C 2 y 2   d x + ∫ C 3 y 2   d x

A primeira integral:

∫ C 1 y 2   d x = ∫ 0 a 0 2 d x = 0

A segunda:

∫ C 2 y 2   d x = ∫ 0 b t 2 d d t a d t = 0

A terceira:

∫ C 3 y 2   d x = ∫ 0 1 b - b t 2 d d t a - a t   d t

Resolvendo a derivada no integrando:

= ∫ 0 1 b - b t 2 - a d t = - a b - b t 3 - 3 b 0 1

Aplicando os limites de integração:

= a 3 b - b 3 = - a b 2 3

Substituindo de volta na equação:

y - = - 1 a b - a b 2 3

Então:

y - = b 3

Resposta

2 a 3 , b 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o Exercício 22 para encontrar o centroide de um quarto de uma região circular de raio a .
Uma lâmina plana com densidade constante ρ x ,y = ρ ocupa uma região do plano x y limitada por um caminho fechado simples C . Mostre que seus momentos de inércia em relação aos eixos são I x = - ρ 3 ∮
Seja D a região limitada por um caminho fechado simples C no plano x y . Utilize o Teorema de Green para demonstrar que as coordenadas do centroide ( x - ,y - ) de D são x - = 1 2 A ∮ C x 2d y y - = -
Utilize o Exercício 25 para achar o momento de inércia de um círculo de raio a com densidade constante em relação a um diâmetro (compare com o Exemplo 4 da Seção 15.5)