Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.7 - Ex. 14
Use uma ferramenta gráfica para desenhar o sólido delimitado pelos paraboloides e .
Passo 1
A questão pede apenas para esboçar a região delimitada pelos paraboloides usando uma calculadora gráfica. Obtemos
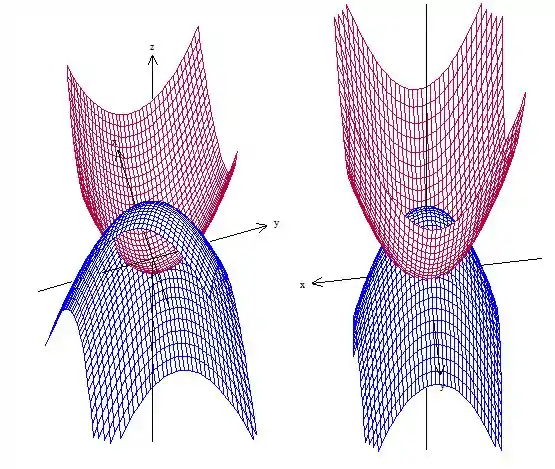
Passo 2
Note que a interseção dos paraboloides ocorre em
Assim,
Limitando os intervalos de apara , temos que
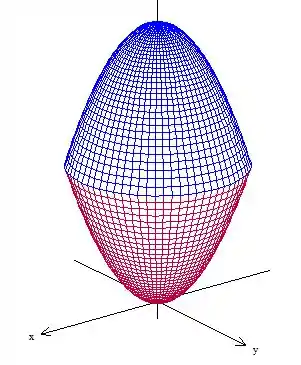
Resposta
Esboço de gráficos.
Exercícios de Livros Relacionados
Faça o esboço do sólido cujo volume é dado pela integral e calcule essa integral. ∫ 0 4 ∫ 0 2 π ∫ r 4 r d z d θ d r
Utilize coordenadas cilíndricas.Determine o volume do sólido que está dentro tanto do cilindro x ² + y ² = 1 ² ² como da esfera x ² + y ² + z ² = 4 ² ² ² .
Utilize coordenadas cilíndricas.Ache o volume da região E limitada pelos paraboloides z = x 2 + y 2 e z = 36 - 3 x 2 - 3 y 2 .Encontre o centroide do E (centro de massa no caso em que a densidade é co
Calcule a integral, transformando para coordenadas cilíndricas. ∫ - 2 2 ∫ - 4 - y 2 4 - y 2 ∫ x 2 + y 2 2 x zd z d x d y
Faça o esboço do sólido cujo volume é dado pela integral e calcule essa integral. ∫ 0 π 2 ∫ 0 2 ∫ 0 9 - r 2 r d z d r d θ