Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.8 - Ex. 1

Faça o esboço do sólido cujo volume é dado pela integral e calcule essa integral.

∫ 0 4 ∫ 0 2 π ∫ r 4 r d z d θ d r

Passo 1

Vamos lá pessoal, temos que resolver uma integral que é o volume de um sólido. Essa integral é a seguinte:

∫ 0 4 ∫ 0 2 π ∫ r 4 r d z d θ d r

Precisamos encontrar quais são as regiões de integração para definir os limites da integral. Além disso, é necessário fazer um esboço do sólido. Veja que a integral dada é em relação as variáveis z , θ e r . O que nos diz que é uma integral em coordenadas cilíndricas.

Passo 2

Vamos fazer o esboço do sólido. Veja as regições de integração da integral:

∫ 0 4 ∫ 0 2 π ∫ r 4 r d z d θ d r

Podemos perceber que a região de integração é dada por coordenadas cilíndricas:

E = r , θ , z |   0 ≤ θ ≤ 2 π ,   0 ≤ r ≤ 4 ,   r ≤ z ≤ 4

Perceba que z será máximo em z = r , e que r máximo é igual a 4 . Então temos que a altura z máxima será 4 com o raio também igual 4 e que a altura irá diminuir linearmente com o raio. Como a integral é de 0 a 2 π podemos afirmar que será feita uma volta completa em torno do eixo z . Então temos o esboço do sólido:

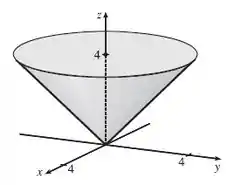
Aqui temos a representação do sólido da região delimitada abaixo pelo cone z = r e acima pelo plano horizontal z = 4 .

Passo 3

Vamos calcular a integral:

∫ 0 4 ∫ 0 2 π ∫ r 4 r   d z d θ d r

Resolvendo a integral de “dentro” temos:

∫ r 4 r   d z = r z ​ r 4

Substituindo os intervalos:

4 r - r 2

Retorn ando a integral:

∫ 0 4 ∫ 0 2 π 4 r - r 2 d θ d r

Resolvendo a integral “de dentro” em relação a θ .

∫ 0 2 π 4 r - r 2 d θ = 4 r θ - r 2 θ 0 2 π

Substituindo os intervalos:

4 r 2 π - r 2 2 π - 0 =   4 r 2 π - r 2 2 π

Resolvendo a última integral:

∫ 0 4 4 r 2 π - r 2 2 π d r = 4 r 2 2 2 π - r 3 3 2 π 0 4

Substituindo os valores dos intervalos em r . Temos:

2 π 2 r 2 - r 3 3 0 4 = 32 - 64 3 2 π

= 64 π 3

Resposta

∫ 0 4 ∫ 0 2 π ∫ r 4 r   d z d θ d r = 64 π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os volumes dos sólidos nos Exercícios 43-48.
Paraboloide e cilindro Encontre o volume da região delimitada superiormente pelo paraboloide z = 9 – x2 – y2, inferiormente pelo plano xy e fora do cilindro x2 + y2 = 1.
Cilindro e paraboloides Encontre o volume da região delimitada inferiormente pelo paraboloide z = x2 + y2, lateralmente pelo cilindro x2 + y2 = 1 e superiormente pelo paraboloidez = x2 + y2 + 1.
Região delimitada por paraboloides Encontre o volume daregião delimitada superiormente pelo paraboloide z = 5 – x2 – y2e inferiormente pelo paraboloide z = 4x2 + 4y2.
Encontre os volumes dos sólidos nos Exercícios 43-48.