Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.8 - Ex. 2
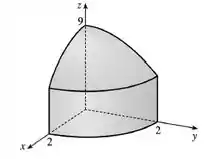
Faça o esboço do sólido cujo volume é dado pela integral e calcule essa integral.
16.
Passo 1
Fala, gente! Tudo belê?
A questão pede o esboço e o cálculo do volume de um sólido definido por essa integral aqui, ó:
Observando essa integral, percebe que ela é delimitada por coordenadas cilíndricas?
Ela tem expressões bem parecidas com as coordenadas polares, olha aqui:
Belê? 😉
Passo 2
Assim, a região de integração do nosso sólido é dada por coordenadas cilíndricas:
Temos o esboço do sólido:
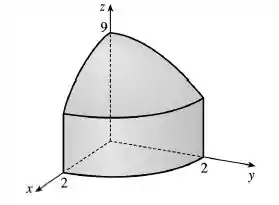
Aqui temos a representação do sólido da região delimitada do primeiro octante envolvido pelo cilíndro circular, delimitado por um parabolóide circular e delimitado abaixo pelo plano.
Passo 3
Agora vamos calcular a integral:
De dentro para fora, primeiro integrando em relação a :
Agora integrando em relação a
Substituindo os limites de integração...
Agora em relação a :
Podemos colocar o para fora da integral, como uma constante:
Assim,
Show? ��
Resposta
