Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.7 - Ex. 22

Utilize coordenadas cilíndricas.

Determine o volume do sólido que está dentro tanto do cilindro x ² + y ² = 1 como da esfera x ² + y ² + z ² = 4   .

Passo 1

Fala, galera!

Essa questão aqui é fogo, hein?

Ela quer, utilizando coordenadas cilíndricas, o volume de um sólido que está dentro do cilindro (azul abaixo) x ² + y ² = 1 e que também está dentro da esfera (vermelha) x ² + y ² + z ² = 4 . Show?

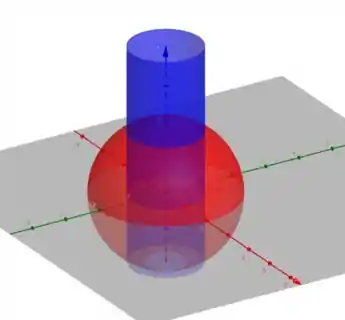
Primeiro, vamos relembrar algumas coordenadas cilíndricas antes de começar a resolver:

x = r   c o s   θ y = r   s e n   θ z = z d V = r   d r   d ϕ   d z

Belê?

Passo 2

Vamos descobrir a região de integração para podermos montar nossa integral tripla (já que temos um volume, certo?).

Com o cilindro, sabemos que nosso r vai de

0 ≤ r ≤ 1

Já que

x 2 + y 2 = r 2

Também temos a esfera

x 2 + y 2 + z 2 = 4

Como sabemos quem é x 2 + y 2 , então

x 2 + y 2 ⏟ r 2 + z 2 = 4

r 2 + z 2 = 4

Então descobrimos que

z = ± 4 - r 2

E temos que angularmente falando, nossa região é o hemisfério positivo da esfera e a parte positiva do cilindro também.

Com isso, temos nossos limites de integração!

E = r , θ , z |   0 ≤ θ ≤ 2 π ,   0 ≤ r ≤ 1 ,   -   4 - r 2 ≤ z ≤ 4 - r 2

Passo 3

Montando nossa integral, ficaremos com:

∫ 0 2 π ∫ 0 1 ∫ -   4 - r 2 4 - r 2 r d z d r d θ

Então, resolvendo de dentro para fora, ou seja, primeiro em relação a z :

∫ -   4 - r 2 4 - r 2 r d z

Colocando r para fora da integral, tratando-o como uma constante, ficaremos com:

r ∫ -   4 - r 2 4 - r 2 d z

Logo,

r z -   4 - r 2 4 - r 2

Substituindo,

r 4 - r 2 - -   4 - r 2

r 4 - r 2 +   4 - r 2

2 r 4 - r 2

Passo 4

Agora integrando em relação a r :

∫ 0 1 2 r 4 - r 2 d r

Colocando 2 para fora da integral como uma constante...

2 ∫ 0 1 r 4 - r 2 d r

Pela técnica da substituição, vamos chamar

u = 4 - r 2

d u = - 2 r d r

d r = d u - 2 r

Assim,

2 ∫ 0 1 r u d u - 2 r  

2 ∫ 0 1 - 1 2 u d u

Jogando a fração também para fora da integral:

2 ⋅ - 1 2 ∫ 0 1 u d u

- ∫ 0 1 u d u

Podemos colocar essa raiz como expoente e assim resolver a integral:

- ∫ 0 1 u 1 2 d u

Como

∫ x n d x = x n + 1 n + 1

Então

- u 3 2 3 2

Pela divisão de frações, invertemos o denominador e passamos a multiplicar com ele:

- 2 3 u 3 2

Simplificando esse expoente, retornando como integral e sabendo quem é nosso u :

- 2 3 u 1 2 + 1

- 2 3 u ⋅ ( u )

- 2 3 4 - r 2 ⋅ ( 4 - r 2 ) 0 1

Agora (ufa!), colocando os limites de integração:

- 2 3 4 - 1 2 ⋅ ( 4 - 1 2 ) - - 2 3 4 - 0 2 ⋅ 4 - 0 2

- 2 3 ⋅ 3 3 + 2 4 ⋅ 4 3

- 2 3 + 16 3

Passo 5

E por fim em relação a θ :

∫ 0 2 π - 2 √ 3 + 16 3   d θ    

Basta colocarmos os números para fora da integral, como já fizemos outras vezes

- 2 √ 3 + 16 3 ∫ 0 2 π d θ      

- 2 √ 3 + 16 3 θ 0 2 π

Colocando os limites de integração, teremos

- 2 3 + 16 3 2 π

Organizando:

- 4 3 π + 32 π 3

Show de bola 😊

Resposta

∫ 0 2 π ∫ 0 1 ∫ -   4 - r 2 4 - r 2 r d z d r d θ = - 4 3 π + 32 π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cilindro e planos Encontre o volume da região delimitadapelo cilindro x2 + y2 = 4 e os planos z = 0 e y + z = 4.
Esfera e cilindro Encontre o volume da região que está dentro da esfera x2 + y2 + z2 = 2 e fora do cilindro x2 + y2 = 1.
Esfera e paraboloide Encontre o volume da região delimitada acima pela esfera x2 + y2 + z2 = 2 e abaixo pelo paraboloide z = x2 + y2.
Como as integrais triplas são definidas em coordenadas cilíndricas e esféricas? Por que alguém poderia preferir trabalharem um desses sistemas de coordenadas a trabalhar em coordenadas retangulares?
Semicilindro infinito Seja D o interior de um semicilindro circular reto infinito de raio 1 , com sua extremidade suspensa a uma unidade acima da origem e seu eixo igual ao raio entre ( 0,0 , 1 ) e ∞