Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.8 - Ex. 13

Utilize coordenadas cilíndricas.

  1. Ache o volume da região E limitada pelos paraboloides z = x 2 + y 2 e z = 36 - 3 x 2 - 3 y 2 .
  2. Encontre o centroide do E (centro de massa no caso em que a densidade é constante).

Passo 1

Vamos lá galerinha, uma questão em que devemos encontrar o volume de uma região entre dois paraboloídes:

z = x 2 + y 2

E

z = 36 - 3 x 2 - 3 y 2

Bem, para isso precisamos identificar onde esses paraboloídes se interceptam para podermos definir a região de integração.Além disso, podemos ver que z está relacionado com x 2 e y 2 o que nos diz que será uma região que forma algum tipo de arco. Ou seja, é razoável considerar que será mais fácil calcular com coordenadas polares.

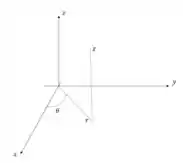
Dessa forma a coordenada r é a distância de cada ponto da origem em valor absoluto, o valor z é a distância em relação ao plano x y e o valor θ é o ângulo que r faz em relação ao eixo x .

Passo 2

  1. Para encontrar o volume da região limitada pelos paraboloides iremos identificar onde eles se interceptam, para isso iremos igualar as coordenadas z de ambos. Sendo assim, temos:

    2. x 2 + y 2 = 36 - 3 x 2 - 3 y 2

    x 2 + y 2 = 9

    Temos então que a região de integração é:

    D = x , y | x 2 + y 2 ≤ 9

    Veja que:

    z = 36 - 3 x 2 - 3 y 2

    Porém, pela teoria das coordenadas polares temos que:

    x 2 + y 2 = r 2

    Então:

    z = 36 - 3 r 2

    E a região de integração é dada por coordenadas cilíndricas:

    E = r , θ , z |   0 ≤ θ ≤ 2 π ,   0 ≤ r ≤ 3 , r 2 ≤ z ≤ 36 - 3 r 2

    Passo 2

    Vamos calcular a integral:

    V = ∫ 0 2 π ∫ 0 3 ∫ r 2 36 - 3 r 2 r d z d r d θ

    Realizando a integral de “dentro” primeiro:

    ∫ 0 2 π ∫ 0 3 r z r 2 36 - 3 r 2 d r d θ = ∫ 0 2 π ∫ 0 3 36 r - 4 r 3 d r d θ

    Agora temos que realizar a integral em relação a r .

    ∫ 0 2 π ∫ 0 3 36 r - 4 r 3 d r d θ =   ∫ 0 2 π 36 r 2 2 - 4 r 4 4 0 3 d θ

    Substituindo os intervalos e resolvendo os valores:

    ∫ 0 2 π 18 r 2 - r 4 0 3   d θ =   ∫ 0 2 π 18 ( 3 ) 2 - 3 4 0 3   d θ

    ∫ 0 2 π 81   d θ = 81   ∙   2 π

    2 π ∙ 81 = 16 2 π

    Passo 3

  2. Agora precisamos calcular o centroide. Para isso precisaremos da da massa que é uma constante k , referente a densidade multiplacada pelo volume. E como sabemos onde está o centro de massa?

O centro de massa está localizado em:

x - = M y z m   ; y - = M x z m ; z - = M x y m

Para a densidade constante K , temos m = K V = 162 π K

pela letra (a), e como a região é homogênea e simétrica temos:

M y z = M x z = 0

Para encontra M x y temos que fazer:

M x y = ∫ 0 2 π ∫ 0 3 ∫ r 2 36 - 3 r 2 z K r d z d r d θ =

Podemos passar tudo que é constante para fora da integral e resolver a integral “mais interna”:

K ∫ 0 2 π ∫ 0 3 r z 2 2 r 2 36 - 3 r 2 d r d θ

Aplicando os limites de integração e simplificando temos:

K 2 ∫ 0 2 π ∫ 0 3 r 36 r - 4 r 2 2 - r 4 d r d θ =   K 2 ∫ 0 2 π ∫ 0 3 8 r 5 - 216 r 3 + 1296 r   d r d θ =  

Resolvendo a integral em relação a r :

K 2 ∫ 0 2 π 8 6 r 6 - 216 4 r 4 + 1296 2 r 2 0 3 d θ

Realizando as substituições necessárias:

∫ 0 2 π 8 6 3 6 - 216 4 3 4 + 1296 2 3 2 0 3 d θ =   K 2 ∫ 0 2 π 2430 d θ

Reallizando a última integral:

K 2 ∫ 0 2 π 2430 d θ = 2430 ∙   2 π = 2430 π K  

Temos então:

x , - y , - z - = M y z m , M x z m , M x y m = 0,0 , 2430 π K 162 π K  

Resposta

  1. V = 16 2 π
  2. x , - y , - z - = 0,0 , 2430 π K 162 π K  
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva a equação em coordenadas cilíndricas.(a) 3 x + 2 y + z = 6 (b) - x 2 - y 2 + z 2 = 1
Escreva a equação em coordenadas cilíndricas.(a) z = x 2 + y 2 (b) x 2 + y 2 = 2 y
Esboce o sólido descrito pelas desigualdades dadas. 0 ≤ θ ≤ π / 2 ,r ≤ z ≤ 2
Esboce o sólido descrito pelas desigualdades dadas. 0 ≤ r ≤ 2 ,- π 2 ≤ θ ≤ π 2 ,0 ≤ z ≤ 1
Utilize coordenadas cilíndricas.Calcule ∭ E x 2 + y 2 d V , onde E é a região que está dentro do cilindro x 2 + y 2 = 16 e entre os planos z = - 5 e z = 4 .