Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.2 - Ex. 23

Use a forma da definição de integral dada no Teorema 4 para calcular a integral.

∫ 0 2 ( 2 - x ² ) . d x

Passo 1

Fala aí! tudo certinho?

Nesse problema temos que aplicar o teorema 4 para calcular a integral

∫ 0 2 ( 2 - x ² ) . d x

Lembra como fazemos isso?

Muito bem galera, vamos relembrar o Teorema 4:

Bora lá!

Passo 2

Usando como base este Teorema:

∫ 0 2 ( 2 - x ² ) . d x = lim n → ∞ ⁡ ∑ i = 1 n ( 2 - x i ² ) . ∆ x

Precisamos saber de duas coisas, x i   e   ∆ x . Começando por ∆ x :

∆ x = 2 - 0 n = 2 n

E agora x i :

x i = 0 + i . 2 n = 2 i n

Colocando no limite:

∫ 0 2 ( 2 - x ² ) . d x = lim n → ∞ ⁡ ∑ i = 1 n 2 - 2 i n 2 . 2 n

∫ 0 2 ( 2 - x ² ) . d x = lim n → ∞ ⁡ ∑ i = 1 n 2 - 4 i 2 n 2 . 2 n

Como o valor de n não vai variar podemos tirá-lo do somatório:

∫ 0 2 ( 2 - x ² ) . d x = lim n → ∞ ⁡ 2 n . ∑ i = 1 n 2 - 4 i 2 n 2

Separando os termos dentro do somatório:

∫ 0 2 ( 2 - x ² ) . d x = lim n → ∞ ⁡ 2 n . ∑ i = 1 n 2 - ∑ i = 1 n 4 i 2 n 2

Vamos pensar! O termo 2 será somado n vezes, concordam?

∫ 0 2 ( 2 - x ² ) . d x = lim n → ∞ ⁡ 2 n . 2 n - ∑ i = 1 n 4 i 2 n 2

Agora sobrou mais um termo constante dentro do somatório, podemos tirá-lo, certo?

∫ 0 2 ( 2 - x ² ) . d x = lim n → ∞ ⁡ 2 n . 2 n - 4 n 2 ∑ i = 1 n i ²

Agora vamos fazer a distributiva:

∫ 0 2 ( 2 - x ² ) . d x = lim n → ∞ ⁡ 4 - 8 n 3 ∑ i = 1 n i ²

Estamos acabando!

Passo 3

Só precisamos saber ∑ i = 1 n i ² , mas o livro já nos disse a resposta pra isso:

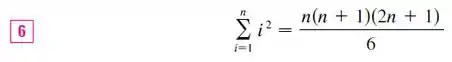
Vamos substituir:

∫ 0 2 ( 2 - x ² ) . d x = lim n → ∞ ⁡ 4 - 8 n 3   . n ( n + 1 ) ( 2 n + 1 ) 6

Reorganizando para facilitar a identificar o limite:

∫ 0 2 ( 2 - x ² ) . d x = lim n → ∞ ⁡ 4 - 8 6   . n ( n + 1 ) ( 2 n + 1 ) n 3

∫ 0 2 ( 2 - x ² ) . d x = lim n → ∞ ⁡ 4 - 4 3   . n n n + 1 n 2 n + 1 n  

Mesma coisa, certo? Só mexi um pouquinho na cara da equação:

∫ 0 2 ( 2 - x ² ) . d x = lim n → ∞ ⁡ 4 - 4 3   . 1 . 1 + 1 n 2 + 1 n  

Quando n → ∞ , o termo 1 n → 0 , concordam? Vamos substituir:

∫ 0 2 ( 2 - x ² ) . d x = 4 - 4 3   1 2 = 4 - 8 3

Então

∫ 0 2 ( 2 - x ² ) . d x = 4 3

E aí! entendeu tudo? Responde Aí!

Resposta

∫ 0 2 ( 2 - x ² ) . d x = 4 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A leitura do odômetro de uma motocicleta em intervalos de 12 segundos é mostrada na tabela a seguir.Estime a distância percorrida pela motocicleta durante esse período, usando a velocidade no começo d
Alguns sistemas algébricos computacionais têm comandos que traçam retângulos aproximantes e calculam as somas de suas áreas, no mínimo se x i * é um extremo esquerdo ou direito.Se f x = x , 1 ≤ x ≤ 4
Se f x = sen ⁡ sen ⁡ x ,0 ≤ x ≤ π / 2 , use os comandos discutidos no Exercício 9 para encontrar as somas esquerda e direita para n = 10 , 30 e 50 .Ilustre fazendo o gráfico dos retângulos da parte (a
Com uma calculadora programável (ou um computador), é possível calcular as expressões para a soma das áreas dos retângulos aproximantes, mesmo para valores grandes de n , usando looping. (Em uma TI us
Com uma calculadora programável (ou um computador), é possível calcular as expressões para a soma das áreas dos retângulos aproximantes, mesmo para valores grandes de n , usando looping. (Em uma TI us