Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 6.2 - Ex. 3g

Ache o domínio e esboce o gráfico.

f (x) = |ln x|

Passo 1

Para resolver essa questão, vamos primeiro lembrar que o logaritmo pode ser escrito também na forma:

y = ln x harr e^y = x

Onde x > 0 , ou seja, x não pode assumir valores negativos.

Assim, para sabermos o domínio de um logaritmo temos que analisar a condição x > 0 , que nesse caso é:

x > 0

Assim o domínio dessa função é:

D = {x in R | x > 0}

Passo 2

Para construir o gráfico vamos admitir valores de x . Por exemplo:

y = |ln x|

x = 1 -> y = |ln 1| = |0| = 0

x = 2 -> y = |ln x| = |ln 2| = |0,693| = 0,693

x = 3 -> y = |ln 3| = |1,099| = 1,099

Agora vamos organizar os dados em uma tabela,

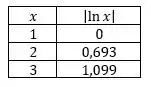
Agora é só colocar esses pontos no gráfico:

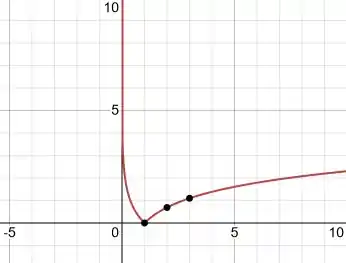
Resposta

D = {x in R | x > 0}

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

39- Qual é a idade de uma amostra de carvão na qual 90% do carbono-14 originalmente presente já decaiu?
40- Esfriamento de uma torta Uma torta de maçã, cuja temperatura interna era de 220ºF ao ser retirada do forno, foi colocada em uma varanda em que a temperatura era de 40ºF para esfriar. Quinze minuto
A razão log 4 ⁡ x log 2 ⁡ x tem um valor constante. Qual é esse valor? Justifique sua resposta.
As funções f ( x )=l n5 xeg ( x )=l n3 x diferem por uma constante. Que constante é essa? Justifique sua resposta.
Como f x = log x ⁡ 2 se compara com g x = log 2 ⁡ x ? Eis aqui uma forma de saber. Use a equação log a ⁡ b= ln ⁡ bln ⁡ a para expressar f ( x ) e g ( x ) em termos de logaritmos naturais. Trace, em um