Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.1 - Ex. 2
Use a fórmula do comprimento de arco para achar o comprimento da curva , . Verifique o seu resultado observando que a curva é um quarto de círculo.
Passo 1
Olá, meu querido amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
A atividade é bem direta sobre o que ela quer, iremos aplicar a fórmula de comprimento de arco para encontramos o comprimento da curva dada no intervalo dado.
Abaixo vamos dar uma olhada na curva que iremos trabalhar:
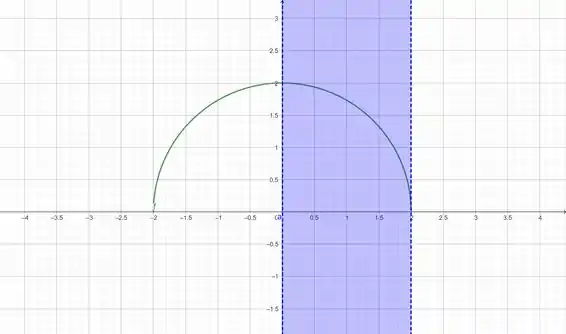
A curva é a que está dentro da região azul.
Já a fórmula que iremos aplicar é a:
Passo 2
Para a nossa situação, , e
Derivando:
Agora vamos substituir na fórmula:
Ufa, chegamos no mesmo resultado!!!
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 23 a 26, use a regra de Simpson com n = 8 para aproximar até quatro casas decimais o comprimento de arco. (24) O arco da curva co-seno, da origem ao ponto ( π 3 , 1 2 ) .
Nos exercícios de 23 a 26, use a regra de Simpson com n = 8 para aproximar até quatro casas decimais o comprimento de arco. (23) O arco da curva seno, da origem ao ponto ( π ,0 ) .
Nos exercícios de 23 a 26, use a regra de Simpson com n = 8 para aproximar até quatro casas decimais o comprimento de arco. (25) O arco da curva y = x 3 3 , da origem ao ponto ( 1 , 1 3 ) .
Se f x = ∫ 0 x s e n ( t )d t , ache o comprimento do arco do gráfico de f do ponto x = 0 ao ponto x = π 2 .
Nos Exercícios de 1 a 4, uma partícula se move aobre uma reta horizontal. Ache a força exercida na partícula se ela tiver a massa e a aceleração dadas (1) A massa é de 50g ; a aceleração é de 5c m / s