Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.3 - Ex. 25

Nos exercícios de 23 a 26, use a regra de Simpson com n = 8 para aproximar até quatro casas decimais o comprimento de arco. (25) O arco da curva y = x 3 3 , da origem ao ponto ( 1 , 1 3 ) .

Passo 1

O primeiro passo é descobrirmos os passo de integração. Para isso fazemos:

∆ x = 1 - 0 n = 1 8

1 3 n = 1 3 * 8 = 1 24

Então, se f x = x 3 / 3   → f ' x = x ² :

f x = ∫ 0 1 1 + ( x ² ) ²   d x = 1 24 f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + 2 f x 4 + 4 f x 5 + 2 f x 6 + 4 f x 7 + f x 8  

Passo 2

Vamos montar uma tabela com os valores encontrados.

∑ i = 0 8 k i f ( x i ) = 2

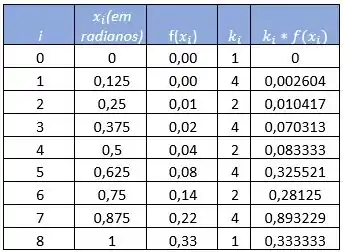
Voltando a integral temos:

∫ 0 1 1 + ( x ² ) ²   d x ≈ 1 24 2 ∫ 0 1 1 + ( x ² ) ²   d x ≈ 0,08333

Resposta

O arco da f x é igual a 0,08333 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o comprimento do arco da curva 8 y = x 4 + 2 x - 2 do ponto onde x = 1 até o onde x = 2 .
Use o Teorema 6.3.3 para encontrar o comprimento do arco da curva y 3 = 8 x 2 do ponto ( 1 ,2 ) ao ponto ( 27 ,18 ) .
Calcule o comprimento do segmento de reta x + 3 y = 4 do ponto ( - 2 ,2 ) ao ponto ( 4 ,0 ) por três métodos: (a) use a fórmula da distância. (b) use o Teorema 6.3.2. (c) use o Teorema 6.3.3.
Ache o comprimento do arco da curva y = 1 3 x ( 3 x - 1 ) do ponto onde x = 1 ao ponto onde x = 4 .
Calcule o comprimento do segmento de reta y = 3 x do ponto ( 1 ,3 ) ao ponto ( 2 ,6 ) por três métodos: (a) use a fórmula da distância. (b) use o Teorema 6.3.2. (c) use o Teorema 6.3.3.