Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 19
Use uma das fórmulas em (5) para achar a área sob um arco da cicloide , .
Passo 1
Fala aí, galerinha! Tudo tranquilo?
A questão pede para acharmos a área sob o arco da cicloide com equações paramétricas:
,
Usando uma das fórmulas dadas no livro como Equação 5:
Aqui na nossa resolução vamos escolher a equação do meio:
Então vamos usar as equações já parametrizadas em do arco da cicloide que o enunciado nos deu para parametrizarmos a equação acima e calcular o valor da integral de linha.
Vamos lá!
Passo 2
A curva no ciclo de a sai do ponto e vai até e tem todos os seus valores positivos nesse ciclo. Esboçando a curva temos algo do tipo:
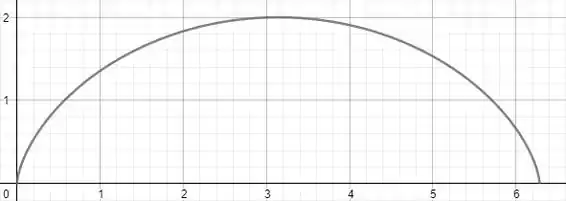
Ainda temos uma curva aberta. Para fechar, vamos usar outra curva que vamos chamar de . A curva liga os pontos e e coincide com o eixo , assim a gente tem uma região fechada e faz sentido o cálculo da área.
Vamos parametrizar essa nova curva por:
Para termos uma orientação positiva no cicloide, vamos ter a variação de a , assim vamos estar percorrendo a curva no sentido anti-horário.
Passo 3
Então para calcular a área vamos usar , vamos chamar essa curva de , então a área pode ser dada por
Como dividimos em duas curvas, ficamos com a soma:
Trocando nossas variáveis pelos nossos parâmetros:
- Para :
- Para :
Então nossa integral fica:
Como temos um menos na frente, podemos sumir com ele invertendo os limites de integração:
Usando:
Ficamos com:
Integrando em e aplicando os limites de integração: