Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 8.1 - Ex. 6

6) Seja K a região hachurada; γ a poligonal ABCD orientada no sentido anti-horário; γ1 a poligonal EHGF orientada no sentido horário; γ2 a poligonalXWZY orientada no sentido horário. Prove que

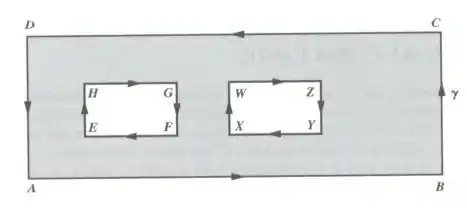
Prove que

Passo 1

Pela mesma ideia do exercício 2 vamos resolver este. Naquele exercício tínhamos

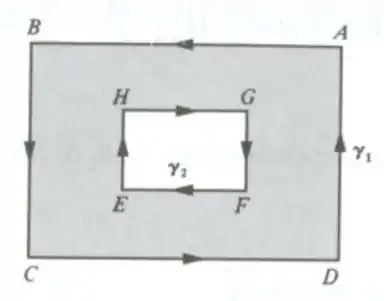
E cortamos a região em 2

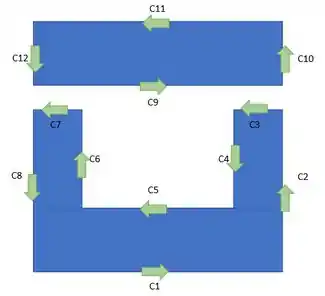
E percebemos que pelo teorema de Green

Passo 2

Neste exercício, se recortamos

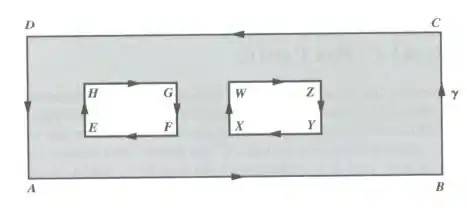
Em varias partes quadradas com orientação anti-horaria, veremos que as curvas internas vão se cancelar, sobrando apenas a curva exterior e as curvas que margeiam o vazio. Logo percebemos que o teorema de green diz é : O fluxo que atravessa a superfície interior é igual ao trabalho ao percorrer a borda dessa superfície, mesmo que a borda e a superfície sejam disformes.

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Aplique o teorema de Green para calcular as integrais nos Exercí-cios 21-24 ∮ C y 2 d x + x 2 d y C: O triângulo limitado por x = 0 , x + y = 1 , y = 0 .

Encontre o fluxo exterior do campo F = 3 x y - x 1 + y 2 i + e x + t g - 1 ⁡ y j através da cardioide r = a ( 1 + c o s ⁡ θ ) , a0 .

Encontre a circulação em sentido anti-horário de F = (y + ex ln y)i+ (ex/y)j ao redor da fronteira da região que está delimitada superiormente pela curva y = 3 – x2 e inferiormente pela curvay = x4 +

Encontre a circulação em sentido anti-horário e o fluxo exterior do campo F = (–sen y)i + (x cos y)j ao redor e sobre oquadrado cortado do primeiro quadrante pelas retas x = p/2 ey = p/2.

Nos Exercícios 19 e 20, encontre o trabalho realizado por F paramover uma partícula uma vez em sentido anti-horário ao redor dacurva dadaF = 2xy3i + 4x2y2jC: A fronteira da região “triangular” no prim