Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 22

Use um gráfico, com auxílio de uma ferramenta gráfica, para estimar as coordenadas do ponto mais baixo e do ponto mais à esquerda na curva

x = t 4 - 2 t

y = t + t 4

A seguir, use o cálculo para encontrar as coordenadas exatas.

Passo 1

Eaee, belezinha??? Bom... o enunciado nos deu as sequintes equações parametrizadas:

x = t 4 - 2 t

y = t + t 4

Primeiramente queremos estimar as coordenadas do ponto mais à esquerda e mais abaixo da curva.

Para isso, o enunciado nos pede para utilizarmos uma ferramenta gráfica para plotar.

Em seguida, deveremos calcular esses pontos, sem auxílio do gráfico.

Nesse caso, basta a gente fazer a derivada d x d t igual a zero para encontrarmos o ponto mais à esquerda.

E, igualarmos a derivada d y d t a zero para encontrarmos o ponto mais abaixo.

Agora bora lá!! 😉

Passo 2

Bom, primeiramente, vamos plotar o gráfico desse negócio aí:

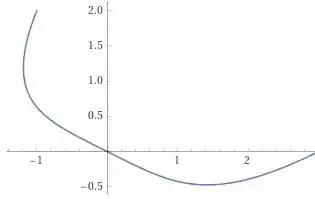
Olhando aí, parece que o ponto mais a esquerda da curva é o ponto

P 1 = ( - 1,2   ; 3,1 )

E o ponto mais baixo é o ponto

P 2 = ( 0,7   ;   - 0,3 )

Só na base do olhômetro mesmo.

Passo 3

Agora pra testar se a gente tá bom de olho e descobrir as coordenadas exatas desses pontos, é só a gente descobrir o ponto em que a reta tangente é vertical (para saber o ponto mais a esquerda) e o ponto em que a reta tangente é horizontal (para saber o ponto mais baixo).

E sabemos que a reta tangente é vertical quando

d x d t = 0

E é horizontal quando

d y d t = 0

Então, vamos achar essa derivada, igualar a zero para encontrar o valor de t em que isso ocorre e depois substituir na parametrização da curva para encontrar o ponto correspondente.

Passo 4

Temos que a equação de x é dada por:

x = t 4 - 2 t

Fazendo a derivada e igualando a zero, temos:

d x d t = 4 t 3 - 2 = 0

t 3 = 2 4

t 3 = 1 2

t = 1 2 3

Passo 5

Substituindo t = 1 2 3 na parametrização da curva, temos:

x 1 2 3 = 1 2 3 4 - 2 1 2 3

x 1 2 3 = - 1,19

E, para y :

y 1 2 3 = 1 2 3 + 6 1 2 3 4

y 1 2 3 = 3,17

Portanto, a reta tangente é vertical no ponto

P 1 = ( - 1,19   ; 3,17 )

E essas são as coordenadas exatas do ponto mais a esquerda da curva.

Bem parecido com o que vimos antes, né?

Passo 6

Agora vamos descobrir o ponto mais baixo, temos que:

y = t + 6 t 4

Fazendo a derivada em relação a t e igualando a zero:

d y d t = 1 + 24 t 3 = 0

t 3 = - 1 24

t = - 1 24 3

t = - 1 2 3 3

Passo 7

Substituindo t = - 1 24 3 na parametrização da curva, temos:

x - 1 24 3 = - 1 24 3 4 - 2 - 1 24 3

x - 1 24 3 = 0,7

E

y - 1 24 3 = - 1 24 3 + 6 - 1 24 3 4

y - 1 24 3 = - 0,26

Portanto, a reta tangente é horizontal no ponto

P 2 = ( 0,7 ; - 0,26 )

E essas são as coordenadas exatas do ponto mais a esquerda da curva.

Também são bem parecido com o que vimos antes, né?

Resposta

Pelo gráfico as coordenadas mais a esquerda e mais baixa são

P 1 = ( - 1,2   ; 3,1 )

P 2 = ( 0,7   ;   - 0,3 )

Respectivamente.

E as coordenadas exatas mais a esquerda e mais baixa são

P 1 = ( - 1,19   ; 3,17 )

P 2 = ( 0,7 ; - 0,26 )

Respectivamente.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os pontos na curva onde a tangente é horizontal ou vertical. Se você tiver uma ferramenta gráfica, trace a curva. x = t 3 - 3 t ,y = t 3 - 3 t 2
Encontre os pontos na curva onde a tangente é horizontal ou vertical. Se você tiver uma ferramenta gráfica, trace a curva. x = e sen ⁡ θ ,y = e cos ⁡ θ
Calcule a inclinação da reta tangente para a curva polar dada no ponto especificado pelo valor de θ . r = 1 + 2 c o s θ θ = π 3
Nos Exercícios de 33 a 36, ache a medida, em graus, do ângulo entre as retas tangentes ao par de curvas dadas em todos os pontos de intersecção.33. r = 1 - s e nθ r = 1 + s e nθ
Prove que nos pontos de intersecção das cardioides r = a 1 + s e nθ e r = b ( 1 - s e nθ ) suas retas tangentes são perpendiculares para todos os valores de a e b .