Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 20
Encontre os pontos na curva onde a tangente é horizontal ou vertical. Se você tiver uma ferramenta gráfica, trace a curva.
Passo 1
Bom dia, boa tarde e boa noite, meu querido aluno. Vamos resolver mais uma atividade?
A gente tem a curva parametrizada dada pelas equações:
A gente precisa então encontrar em quais pontos dessa curva parametrizada, a tangente a essa curva é horizontal ou vertical.
Para encontrarmos o que precisamos, deveremos derivar a equação e encontramos o coeficiente angular da reta tangente. Ele é encontrado com essa derivada:
E após encontrarmos esse coeficiente, deveremos fazer o seguinte:
Para que as tangentes sejam horizontais, deveremos ter que:
E para que as tangentes sejam verticais, deveremos ter que:
Isso mesmo, quando for indefinido por conta do zero no denominador.
Passo 2
Toda a curva é traçada para .
O primeiro passo é derivar as funções, e derivando , a gente precisa aplicar a regra da cadeia aqui, já que a gente tem uma composição de função:
E
Se , assim .
Isso implica que os pontos são descobertos substituindo em
Os valores
Temos então que:
Passo 3
E derivando , temos que novamente aplicar a regra da cadeia:
E
Se , assim .
Isso implica que os pontos são:
Passo 4
A curva tem tangentes horizontais em e e tangentes verticais em e .
E a curva é da seguinte forma:
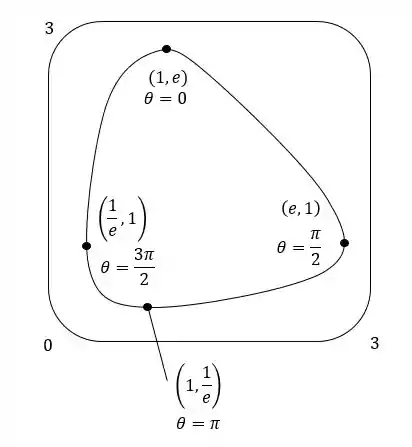
Terminamos por aqui então a nossa resolução meu nobre amigo.
Resposta
A curva tem tangentes horizontais em e e tangentes verticais em e .
