Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 25
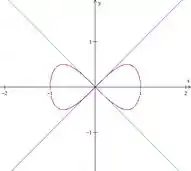
Mostre que a curva
Tem duas tangentes em e encontre suas equações. Esboce a curva.
Passo 1
Olá, meu amigo. Vou te ajudar a resolver essa atividade aqui.
A gente tem a curva parametrizada:
E a gente precisa encontrar duas equações das retas tangentes a está curva no ponto:
A equação da reta tangente a uma curva é:
Onde é o coeficiente linear da reta, e é dado por:
Assim, precisamos encontrar as derivadas de e em relação a e substituir nessa fórmula.
Já os pontos e , são os pontos de tangencia e costumam ser dados no enunciado, aqui eles são:
Passo 2
Vamos começar pela derivada de :
Para isso a gente vai ter que utilizar da regra do produto:
E usando lá aquelas identidades trigonométricas que esse livro parece adorar,
Agora a derivada de :
Substituindo na fórmula
Passo 3
Agora a gente precisa descobrir o valor do parâmetro correspondente ao ponto de tangencia . Para isso é igualar o ponto à parametrização da curva e resolver o sistema.
Daí, tiramos que
ou
Ou seja, temos dois valores possíveis para correspondentes ao ponto .
Passo 4
Substituindo no vetor tangente, temos:
Para
Para :
Assim, temos dois vetores tangentes, logo, vamos ter duas retas tangentes no ponto .
Passo 5
Assim, as equações da reta tangente no ponto ficam:
E
Passo 6
Plotando a curva naquele esquema de usar o Winplot, mas em último caso podemos usar método de ir chutando valores de e ir plotando números e depois ligar os pontos. Além disso, vamos desenhar também as duas retas tangentes, que são duas retas passando pela origem.
Fica tudo assim:
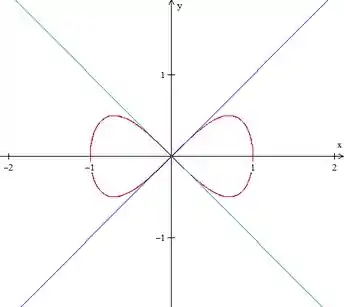
Resposta
As retas tangentes são
E
