Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.5 - Ex. 75

Use um gráfico para dar uma estimativa da área da região que está sob a curva dada. A seguir, encontre a área exata.

y = 2 x + 1 , 0 ≤ x ≤ 1

Passo 1

A questão pede para estimarmos a área sob a curva usando um gráfico e depois para calcularmos a mesma área usando integral.

A curva que temos é:

y = 2 x + 1 , 0 ≤ x ≤ 1

Usando um software gráfico para desenhar o esboço da região, temos o seguinte:

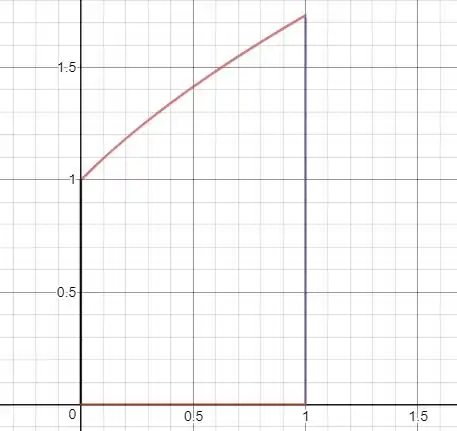
Note que podemos aproximar essa área por um trapézio de base maior 1.7 , base menor 1 e altura 1 . Assim,

A t p z = B + b h 2

A ≈ 1.7 + 1 ⋅ 1 2 = 2.7 2 = 1.35

Passo 2

Agora vamos calcular a integral para obter o valor exato:

A = ∫ 0 1 2 x + 1   d x

Note que aqui podemos usar a técnica da substituição.

Uma boa opção é usar o que tá dentro da raíz, pois assim transformamos a raíz que possui dois termos na raíz de apenas um termo. Além disso, se tomarmos

u = 2 x + 1

A sua derivada que é

u ' = 2

Não depende de x , e isso é importante para que após a substituição tudo esteja escrito em termos da nova variável u .

Para a técnica da substituição devemos pegar parte do termo que está sendo integrado e chama-lo de u .

Então, devemos encontrar d u derivando u em termos de x .

d u = u ' d x

E portanto teremos que:

d x = d u u '

E dessa forma, substituímos a diferencial de x da integral.

Por fim, basta resolver a integral, desfazer a substituição e então substituir os limites de integração.

Ou então, você pode reescrever os limites de integração na variável u , resolver a integral e substituir os limites de integração, sem precisar desfazer a substituição.

Eu vou seguir por esse caminho aqui.

Passo 3

Nossa integral (que representa a área que queremos é):

A = ∫ 0 1 2 x + 1   d x

Vamos fazer a substituição

u = 2 x + 1

E vamos derivar para encontrar seu diferencial d u :

d u = u ' d x

Portanto,

d u = 2 d x

E portanto, teremos que:

d x = d u 2

Para os limites de integração, temos que quando:

x = 0

u = 2 0 + 1 = 1

E que quando:

x = 1

u = 2 1 + 1 = 3

Assim, substituindo teremos:

∫ 0 1 2 x + 1   d x = 1 2 ∫ 1 3 u d u

Transformando em potência para facilitar a integração:

= 1 2 ∫ 1 3 u 1 / 2 d u

Usando a regra da potência para a integral temos:

= 1 2 u 3 2 3 2 1 3

1 2 2 3 u 3 1 3

E por fim, substituindo os limites de integração temos:

= 1 3 27 - 1

= 1 3 ( 3 3 - 1 )

Passo 4

Efetuando a conta, obtemos

1 3 3 3 - 1 ≈ 1.4

Observe que esse resultado não está longe de nossa estimativa, fizemos um bom trabalho!!!

Resposta

A = 1 3 ( 3 3 - 1 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A afirmação a seguir é sempre, às vezes ou nunca verdadeira? A área da região entre os gráficos das funções contínuas y = f x e y = g ( x ) e as retas verticais x = a e x = b ( ab ) é ∫ a b [ f x - g
A O C inscrito na região que vai da parábola y = x 2 até a reta y = a 2 . Determine o limite da razão entre a área do triangulo e a área da região parabólica quando a tende a zero.
Quais das integrais a seguir, se houver alguma, serve para calcular a área da região sombreada mostrada aqui? Justifique sua resposta.a.∫ - 1 1 x - - x d x = ∫ - 1 1 2 x d x ∫ - 1 1 - x - x d x = ∫ -
Suponha que a área da região entre o gráfico de uma função continua positiva f e o eixo x de x = a até x = b seja 4 unidades quadradas. Determine a área entre as curvas y = f ( x ) e y = 2 f ( x ) de
Determine a área da região no primeiro quadrante, limitada à esquerda pelo eixo y , abaixo pela reta x = 2 y , acima à esquerda pela curva x = y - 1 2 e acima à direita pela curva x = 3 - y .