Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.6 - Ex. 107

A O C inscrito na região que vai da parábola y = x 2 até a reta y = a 2 .   Determine o limite da razão entre a área do triangulo e a área da região parabólica quando a   tende a zero.

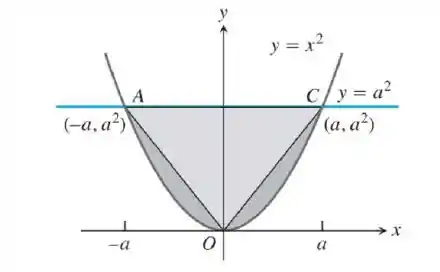
Passo 1

Vamos analisar bem a figura ok?

Perceba que se a gente calcular a área fazendo a

∫ - a a f ( x ) d x

Ou seja, calcular a área em relação à x , a área que estará sendo considerada será a parte de baixo, mas desejamos a parte de cima. Então vamos ter que readaptar a integral para achar a área em relação ao eixo y .

Mas antes, precisamos saber das retas do triangulo. Lembre-se que a equação de uma reta é dada por:

y = y 0 + m ( x - x 0 )

Onde,

m = y 0 - y 1 x 0 - x 1

Tomando y 0 = 0 e y 1 = a 2 , x 0 = 0   e x 1 = a ,   temos que

m = 0 - a 2 0 - a = a

Logo, a equação da reta é:

y = a x .

Passo 2

Temos uma outra observação a fazer: como o gráfico é simétrico em relação ao eixo y calcular

2 ∫ 0 a f ( x ) d x

É suficiente.

Mas como vamos fazer a integral em relação a y vamos obter os limites de integração e o integrando

y = a x .

x = 0 ⇒ y = a e x = a ⇒ y = a 2

E, x = y a .Então nossa integral fica

2 ∫ y = 0 y = a 2 y a d y = 2 y 2 2 a ​ y = 0 y = a 2 = y 2 a ​ y = 0 y = a 2 =   ( a 2 ) 2 a - 0 2 a =   a 2 2 a - 0 2 a = a 4 a - 0 = a 3

Da mesma forma, vamos modificar nossa integral para calcular a com relação ao eixo y .

y = x 2 ⇒ x = 0 ⇒ y = 0

x = a ⇒ y = a 2

x = y

Sendo assim a integral é da forma:

2 ∫ y = 0 y = a 2 y d y = 2 . 2 3 x 3 2 ​ y = 0 y = a 2 = 4 3 x 3 2 ​ y = 0 y = a 2 ⇒ 4 3 a 6 = 4 3 a 3

Fazendo a razão desejada

A t A p = a 3 4 3 a 3 = 3 4

Onde A p : Area da parábola e A t : Area do triangulo

Calculando o limite

l i m a → 0 3 4 = 3 4

Resposta

o limite da razão entre a área do triangulo e a área da região parabólica quando a   tende a zero é 3 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache a taxa de variação da medida da área do Exercício 48 em relação a p quando p = 3 8 .
Ache a área da seção limitada pela curva y = tan 2 ⁡ x , pelo eixo x e pela reta x = 1 4 π .
Ache a área da região limitada pelas três curvas y = x 2 ,y = 8 - x 2e4 x - y + 12 = 0 .
Ache a área da região limitada pela reta x = 4 e pela curva x 3 - x 2 + 2 x y - y 2 = 0 . (Sugestão: resolva a equação cúbica em y em termos de x e expresse y como duas funções de x.)
Ache a área da seção limitada pelas curvas y = sin ⁡ x e y = cos ⁡ x entre dois pontos de interseção consecutivos.