Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.5 - Ex. 50
Calcule a integral indefinida. Ilustre e verifique se sua resposta é razoável fazendo o gráfico da fun��ão e de sua primitiva (tome ).
Passo 1
Fala aí! Tudo certinho? 😉
Essa questão pede pra gente calcular a integral indefinida dada por:
Além disso temos que ilustrar e verificar se nossa resposta é razoável fazendo o gráfico da função e de sua primitiva e tomaremos nassa constante de integração .
Então, vamos nessa.
A ideia aqui será olhar com atenção a função que estamos integrando. Perceba que ela não é uma integral muito simples mas podemos tentar fazer uma substituição simples e verificar se isso ajuda a tornar nossa integral mais fácil de ser resolvida.
Para isso saber se é isso mesmo que devemos fazer, vamos observar se ao derivarmos uma parte da função, aparecerá algo semelhante a outra parte da função.
Vem que vou te mostrar como será isso.
Passo 2
Queremos resolver a seguinte integral:
No cálculo da integral, vamos precisar fazer uma substituição.
Como a derivada da tangente é secante ao quadrado, vamos fazer a substituição:
E sua derivada será:
Desta forma, a integral que era
Se transforma em:
Passo 3
Agora basta resolver essa integral, que se transformou em uma integral de potência. E sua integração será na forma:
Com .
Assim:
Voltando a variável original, lembrando que fizemos
Podemos dizer que:
Maravilha. Integral calculada.
Passo 4
Lembrando que o enunciado nos disse para tomar .
Assim, em vermelho fazemos o gráfico da função e em azul o de sua primitiva:
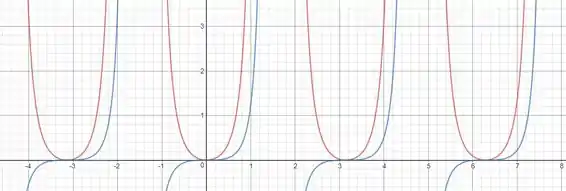
Veja que a curva vermelha é sempre positiva e a curva azul é sempre crescente.
Sempre que a curva azul tem uma tangente horizontal, a curva vermelha se anula e, além disso, as duas são descontínuas no mesmo ponto.
Vemos então que a curva vermelha se comporta como derivada da curva azul, que é exatamente o comportamento de uma função com relação a sua primitiva.
E aí! Entendeu tudo? Responde Aí! 😉
