Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 4
Encontre a área da região sombreada.
Passo 1
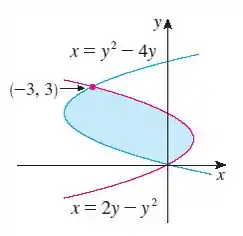
Opa, bora resolver esse problema! Queremos encontrar a área da seguinte região sombreada:
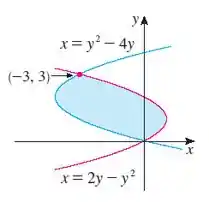
Repara que essa região é a curva menos a curva ?!
Isso porque a curva da direita tem valores maiores de quando comparados a curva da esquerda. Logo, se subtraímos uma da outra vamos ter um positivo.
Temos então:
Mas pra calcular uma área precisamos integrar a função com os limites de integração. Certo?!
Eles vão ser os , nos pontos de intersecção entre as curvas:
Agora escrevemos a integral:
Sabemos que temos que integrar com respeito a pois as curvas estão “de ladinho”!
Passo 2
Agora integramos:
Aplicando os limites de integração:
Prontinho!
Resposta
Exercícios de Livros Relacionados
Desenhe a curva dada (coordenadas polares ). h ) rho^2 = (1)/(1 + sin^2 theta)
Calcule a área da região limitada pela curva dada(coordenadas polares). a )ρ = 2 - cos θ
Calcule a área da intersecção das região limitada pelas curvas dadas em coordenadas polares d )ρ 2 = cos θeρ 2 = sin θ( ρ ≥ 0 )
Calcule a área da região limitada pela curva dada(coordenadas polares). c ) ρ = cos 3 θ
Calcule a área da região limitada pela curva dada(coordenadas polares). b ) ρ 2 = cos θ ( ρ ≥ 0 )