Use um gráfico para encontrar as coordenadas aproximadas dos pontos de intersecção das curvas dadas. A seguir, ache (aproximadamente) a área da região delimitada pelas curvas.
Passo 1
Traçando o gráfico das curvas e , observamos que essas curvas se cruzam quando e .
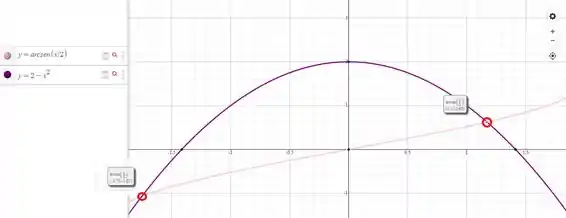
Passo 2
Logo temos que o intervalo de interceção é . Atribuindo e temos que a área entre essas curvas é dada por:
Perceba que desmembramos nossa integral em três pela propriedade da soma e da diferença de integrais. As duas primeiras integrais são integrais que resolvemos pela integração de um polinômio, que é dada por:
Já a última nós teremos que aplicar aplicar a técnica de integração por partes. Para isso precisamos dividir o argumento da integral em duas funções e respectivamente. Feito isso, aplicamos a fórmula para a integração por partes que é dada por :
Ou de forma mais visível, fazemos:
Primeiro então, devemos definir quem vão ser nossas funções. É aconselhável escolher a função mais fácil de derivar para ser ou a mais difícil de se integrar. Assim atribuindo os valores em referência a primeira integral temos:
Derivando e integrando , temos:
Aplicando as funções e suas derivadas na fórmula citada , temos:
Passo 3
Retomando a integral inicial, temos:
Aplicando os valores de e , obtemos um valor aproximado para a área de .