Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.6 - Ex. 57
57. Use o gráfico para encontrar um número tal que
Passo 1
Falaaa... tudo bem??
Nessa questão vamos desenhar o gráfico (como a função é meio estranha e o gráfico não é tão conhecido, então vamos usar algum software) e depois encontramos o número tal que:
Pra isso vamos usar a definição:
Seja uma função definida em algum intervalo . Então
Significa que para todo existe um correspondente número tal que
sempre que
No nosso caso:
Lembrando que:
Se
Então:
Então vamos desenhar no gráfico a função e a reta . Depois vamos ver em que parte elas praticamente se encontramos, pois queremos achar valores de onde a diferença, em módulo, seja menor que .
Passo 2
Reescrevendo após lembrarmos esse nosso conceito de módulo, teremos essa parada aqui:
Somaremos o , para deixarmos essa expressão feia, mais amigável. Vamos lá!
Então nosso objetivo é determinar os valores de para os quais a curva com equação fique entre as retas e
Passo 3
Pelo enunciado da questão, teremos que usar um recurso gráfico. Usarei o meu software de gráfico, porém você decide qual software irá usar.
Apenas lembre de fazer o gráfico da curva (linha azul)
Da reta (linha verde) e das retas (linha vermelha) e (linha laranja).
Repara que a linha azul (linha da função) começa a se aproximar da linha vermelha próximo de , então vamos dar um super zoom no gráfico:
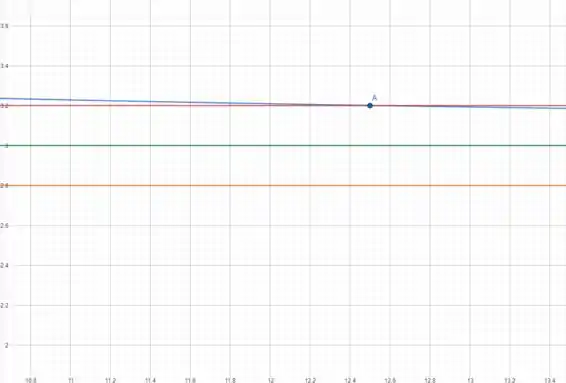
O ponto A é o ponto onde o gráfico da função começa a ficar entre as as retas e . E esse ponto está entre e , portanto. O menor número para o gráfico da função ficar na região entre essas duas retas é o número .