Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.4 - Ex. 2
Use o gráfico de para encontrar um número tal que se então
Passo 1
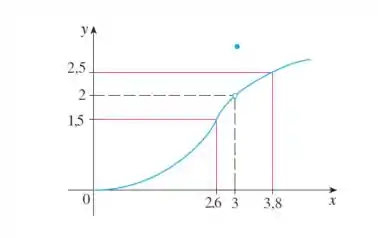
Opa, vamos fazer essa questão! O enunciado nos dá esse gráfico aqui:
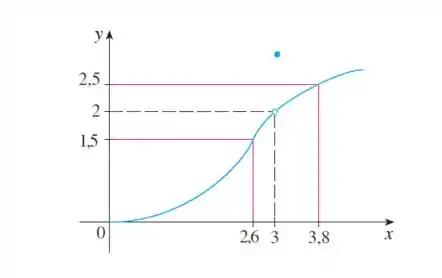
A primeira coisa que podemos observar nesse gráfico é que . Mas vamos ao que interessa!
O enunciado pede pra a gente, a partir do gráfico acima, encontrar um número tal que satisfaça as seguintes condições:
Huuum, isso lembra a alguma coisa, vamos olhar a definição de limite:
Se para todo número houver um número tal que:
Se então
Passo 2
Antes de qualquer coisa, vamos tirar esses carinhas do módulo. Dessa forma vamos ter:
Assim:
Agora fazemos o mesmo pra :
Passo 3
Temos que:
Somando 2 a todos os membros:
Analisando o gráfico, podemos ver que nesse intervalo de , temos:
A gente sabe que:
Somando a todos os membros:
Então podemos concluir que:
E:
Passo 4
Agora vamos estudar as duas possibilidades, lembrando que pelo nosso gráfico temos:
Primeiro faremos :
Nesse caso o esta dentro do nosso intervalo! Mas vamos testar :
Esse valor de não serve, pois temos o está fora do intervalo, então temos .