Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.4 - Ex. 1
- Use o gráfico de para encontrar um número tal que se então .
Passo 1
Eaee, belezinha?? Bom... queremos encontrar um número tal que se
Então
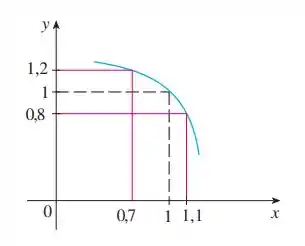
Para isso, o enunciado nos dá o seguinte gráfico:
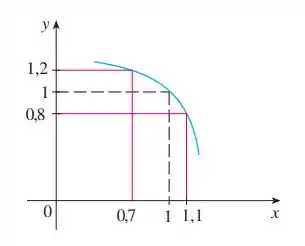
Bom... Aqui iremos utilizar o gráfico em conjunto com a definição de limite.
Pra fazermos essa, temos que lembrarmos da definição de limite, olha só:
Se para todo número houver um número tal que:
Se então
Agora bora lá!! 😉
Passo 2
Como :
Logo,
Analisando o gráfico, podemos ver que nesse intervalo de , temos:
Para o , temos:
Assim,
Passo 3
Agora vamos trabalhar com as equações e .
1° caso:
Então nosso intervalo fica o seguinte:
Isto é,
Opa, esse não serve pois o .
2° caso:
Então nosso intervalo fica o seguinte:
Isto é,
Esse deu bom. Logo,
Resposta
Exercícios de Livros Relacionados
Resolver as inequações em R .n) 3 x - 1 + x1
Resolver as inequações em R .l) 5 2 x - 1 ≥ 1 x - 2
Demonstrar:c) xa se e somente se xa ou x- a , onde a0 .
Resolver as equações em R .g) 9 x - 11 = x
Resolver as inequações em R .p) x - 1 + x - 34 x