Use o método de Newton (Seção 4.7), quando necessário, para aproximar as coordenadas das intersercções das curvas com pelo menos quatro casas decimais; em seguida, use isso para aproximar a área da região.
A região entre os gráficos de e .
Passo 1
Para encontrar a região englobada por curvas, precisamos analisar a região dada e montar a integral:
Ou
E calculá-la.
Mas para descobrir os extremos de integração, muitas vezes precisamos achar a interseção entre curvas, e é aí que entra o método de Newton. Ele diz que usando essa fórmula:
Achamos uma aproximação para que zera a função . E para achar a interseção entre duas funções e a partir desse método, fazemos:
E chamamos:
Aí só usar a fórmulinha. Belezinha? Vamos começar!
Passo 2
Essa é a nossa região:
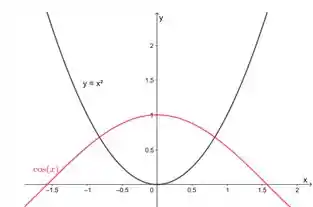
Vemos que a região está limitada por cima pela função e por baixo pela função . Vemos também que nossa região é simétrica em relação ao eixo (os dois lados tem áreas iguais). Já que temos funções de , podemos escrever nossa integral como:
O desafio é achar os extremos de integração. Vamos fazer a interseção entre as curvas:
A solução dessa equação, a gente vai ter que achar usando o método de Newton.
Agora a gente usa a fórmula de Newton até aproximar o valor de com pelo menos quatro casas decimais:
Para chutar um , precisamos dar uma olhadinha no gráfico da região. A gente vê que, na metade direita, a interseção ocorre entre e , vamos começar chutando . Fazendo isso, vemos que e já repetem as mesmas quatro casas decimais:
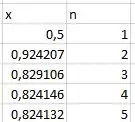
Logo, nosso .
Passo 3
Agora é só calcular a integral: