Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 46a
Use o gráfico para estimar o valor de com uma casa decimal
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente usar o gráfico da função para estimar o valor do limite de quando tende a infinito:
Usando uma casa decimal.
Então, o que nós vamos fazer é plotar o gráfico da função no plano cartesiano e analisar o comportamento dessa curva quando vai para infinito.
Vamos lá!
Passo 2
Esboçando o gráfico de , temos:
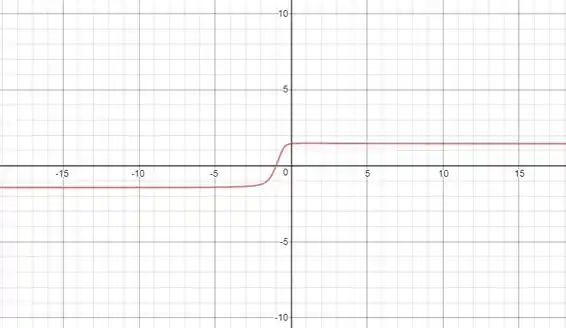
Para encontrarmos o limite analisando o gráfico é possível observar que cada quadrado maior possui unidades de lado e cada quadrado menor possui 1 unidade de lado.
Então, podemos ver que o gráfico faz uma assíntota horizontal, ou seja, quando , a função tende a (pois pode-se observar que a assíntota não chega exatamente à reta ).
E expressando matematicamente, temos:
Valeu, galera! Até a próxima! 😉