Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.1 - Ex. 64

Use o gráfico para estimar os valores críticos.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você??Vamos analisar o que nosso probleminha está falando. Bom, ele nos pede para acharmos os valores críticos para a nossa f(x) através da análise do gráfico dela.

Essa é uma função que não é tão simples de graficar. Dessa forma, vamos usar um recurso gráfico para montar o gráfico e a partir dele encontrar os valores críticos, que vão ser aqueles nos quais a derivada é zero, ou seja, pontos de máximo e mínimo locais.

Passo 2

Fazendo o gráfico da função

Temos:

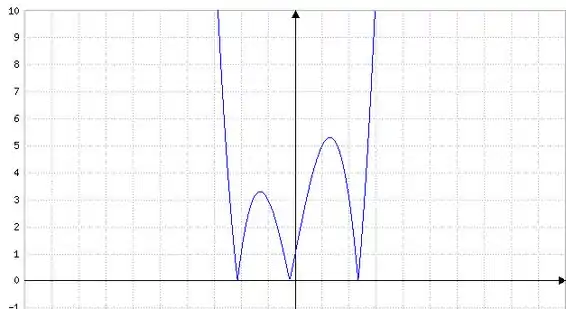
Agora, vamos analisar onde as nossas derivadas são zero.

Podemos ver bem que ali perto do nosso temos um máximo local e do nosso também. Nesses pontos, temos uma inclinação da tangente praticamente nula, o que nos permite dizer que a derivada naqueles pontos é zero.

Feito isso, vamos agora usar esses valores para achar nossos valores críticos.

Resposta

Valores críticos

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os pontos críticos da função dada e classifique-os (a classificação refere-se a ponto de máximo local, ponto de mínimo local ou ponto de inflexão).e) f x = x 4 - 4 x 3 + 6 x 2 - 4 x + 1

Determine os pontos críticos da função dada e classifique-os (a classificação refere-se a ponto de máximo local, ponto de mínimo local ou ponto de inflexão).c) h x = x 3 - 3 x 2 + 3 x - 1

Determine os pontos críticos da função dada e classifique-os (a classificação refere-se a ponto de máximo local, ponto de mínimo local ou ponto de inflexão).f) g x = x 2 e - 5 x

Determine os pontos críticos da função dada e classifique-os (a classificação refere-se a ponto de máximo local, ponto de mínimo local ou ponto de inflexão).a) f x = x 4 4 - x 3 - 2 x 2 + 3

Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada