Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 67
O economista chefe do governo anunciou que o déficit nacional está crescendo, mas a uma taxa decrescente. Interprete a afirmação em termos de uma função e suas primeira e segunda derivada.
Passo 1
Bom galera, vamos considerar que o déficit nacional é um função .
E temos que a taxa com que é a nossa .
Já a taxa com que a cresce é a nossa .
Passo 2
Beleza, o economista disse que o déficit nacional está aumentando, então:
Show de bola, agora ele também disse que a taxa cresce mas com uma taxa decrescente
Portanto, a taxa com que a derivada cresce é negativa, logo, a segunda derivada é negativa.
Um exemplo de função assim é essa aqui ó
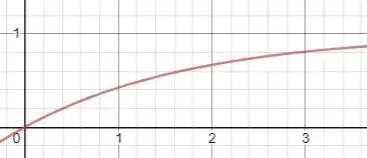
Repara que essa função tá sempre crescendo, mas cada vez mais ela cresce menos.
Resposta
Exercícios de Livros Relacionados
Seja f x = e - 1 x 2 s e x ≠ 0 0 s e x = 0 Calcule f ' 0 , pela definiçãoDetermine f ' Esboce o gráfico, calculando, para isto, todos os limites necessários
Calcule.underset(x - + oo)(lim) (e^x)/(x^3)
Seja n ≥ 2 um natural dado. Prove que x n - 1 ≥ n x - 1 para todo x ≥ 1 .(Sugestão: Verifique que f x = x n - 1 - n x - 1 é estritamente crescente em 1 , + ∞ .)
Mostre que, para todo x0 , tem-secos x1 - (x^2)/(2) sen xx - (x^3)/(3 !)
Mostre que, para todo x0 , tem-se sen xx - x 3 3 ! + x 5 5 ! 0sen x - x - x 3 3 !x 5 5 ! (Sugestão: Utilize o item (b) do Exercício 10 e o item (a) acima.)