Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 13
Use o gráfico da função para dizer o valor de cada limite, se existir. Se não existir, explique por quê .
- (b) (c)
Passo 1
Falaeee, belezinha?? Bom... a questão nos dá a seguinte função:
Com isso, a questão quer que tracemos o seu gráfico a fim de dizer o valor de cada limite, se existir.
a)
b)
c)
Se não existir, devemos explicar o porquê.
Lembrando que quando tem o sinal de menos, estamos calculando o limite de tendendo a pela esquerda. Quando tem o sinal de mais, estamos calculando o limite de tendendo a pela direita.
Também devemos lembra que pra um limite existe, os limites laterais naquele ponto devem existir e devem ser iguais.
Para isso, devemos traçar o gráfico com ajuda de algum software matemático para podermos analisar em seguida. Aqui iremos utilizar o GeoGebra para nos ajudar com o grafico.
E aí? Bora lá?? 😉
Passo 2
O gráfico de é dado por:
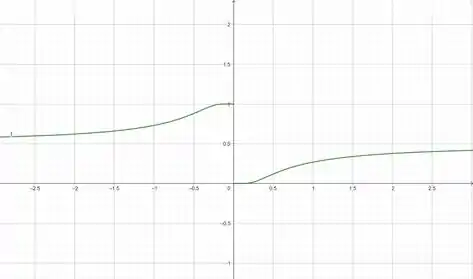
Analisando um pouco o gráfico...
Repara que quando está se aproximando de pela esquerda, o valor de está se aproximando de .
Já pela esquerda, o valor de está se aproximando de 0.
Então temos limites laterais diferentes. Podemos dizer até que temos uma descontinuidade na função (quando tem esses saltos e as partes do gráfico não se juntam).
Passo 3
- Para , analisamos o gráfico começando pela esquerda, assim quando se aproxima de . Portanto:
- Para , analisamos o gráfico começando pela direita, assim quando , se aproxima de. Portanto:
- Como os limites laterais são diferentes (observe os resultados obitdos em (a) e em (b)) e por definição temos que:
se e somente se e .
Concluimos que não existe.
Resposta
a) 1
b) 0
c) não existe