Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.2 - Ex. 60

Use um gráfico do integrando para conjecturar o valor da integral. Então, utilize os métodos desta seção para demonstrar que sua conjectura está correta.

∫ 0 2 sin ⁡ 2 π x cos ⁡ 5 π x d x

Passo 1

Primeiro, vamos esboçar o gráfico da função no intervalo dado, que fica o seguinte

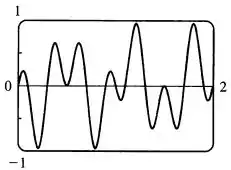
Tá lembrado o que é a integral? Não? Então vou te lembrar, a integral nada mais é do que a área embaixo de uma curva, mas você deve se lembrar que se o gráfico da função estiver no terceiro ou quarto quadrante do eixo cartesiano, estamos falando da área acima da curva, então se a gente olhar o gráfico podemos concluir que as áreas somadas no primeiro quadrando da exatamente o mesmo valor que a área acima do gráfico no quarto quadrante. Logo, matematicamente, podemos concluir o seguinte

∫ 0 2 sin ⁡ 2 π x cos ⁡ 5 π x d x = 0

Passo 2

Agora, vamos calcular esta integral analiticamente, pra isso, você precisa lembrar da seguinte propriedade trigonométrica: sin ⁡ A cos ⁡ B = 1 2 sin ⁡ A - B + sin ⁡ A + B , então, substituindo

∫ 0 2 sin ⁡ 2 π x cos ⁡ 5 π x d x = 1 2 ∫ 0 2 sin ⁡ 2 π x - 5 π x + sin ⁡ 2 π x + 5 π x d x = 1 2 ∫ 0 2 sin ⁡ - 3 π x + sin ⁡ 7 π x d x = 1 2 1 3 π cos ⁡ - 3 π x - 1 7 π cos ⁡ 7 π x 0 2 = 1 6 π cos ⁡ - 3 π x - 1 1 4 π cos ⁡ 7 π x 0 2 = 0

Resposta

∫ 0 2 sin ⁡ 2 π x cos ⁡ 5 π x d x = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área total da região delimitada pela curva y = 2 ln ⁡ x x e o eixo x de x = 1 até y = e .
Determine a área total da região delimitada pela curva x = y 2 3 e pelas retas x = y e y = - 1 .
Determine os valores extremos de f x = x 3 - 3 x 2 e a área da região delimitada pelo gráfico de f e pelo eixo x .
Ache o centroide da região x = 1 a x = π 2 , limitada pela curva y = c o s x e pelo eixo x.
Ache o centroide da região limitada pelo eixo y e pelas curvas y = s e nx - cos ⁡ x e y = s e nx + cos ⁡ x de x = 0 a x = π 2 .