Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.Revisão - Ex. 107

Ache o centroide da região limitada pelo eixo y e pelas curvas y = s e n   x - cos ⁡ x e y = s e n   x + cos ⁡ x de x = 0 a x = π 2 .

Passo 1

O problema pede para acharmos o centro de massa da região limitada pelo eixo y e pelas curvas y = s e n   x - cos ⁡ x e y = s e n   x + cos ⁡ x . O esboço dessa região é dado a seguir:

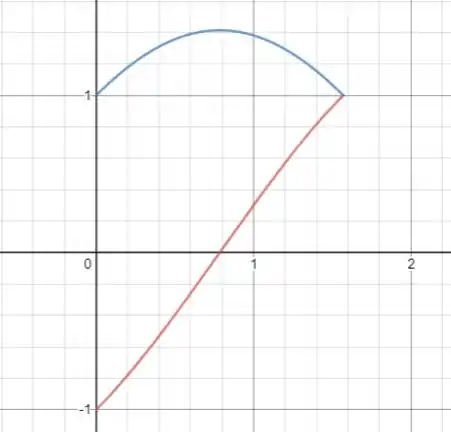
Note que nesse caso não temos nenhuma simetria significativa, então teremos que calcular as duas coordenadas do centro de massa na raça. Para isso, temos que lembrar que as coordenadas do centro de massa de uma região entre as curvas y = g ( x ) e y = f ( x ) é dado por

x - = 1 A ∫ x   f x - g x   d x           e               y - = 1 A ∫ 1 2 f x 2 - g x 2   d x ,

onde A é a área da região:

A = ∫ f x - g x   d x

Neste caso, temos que f x = s e n   x + cos ⁡ x e g x = s e n   x - cos ⁡ x . Assim,

f x - g x = 2 cos ⁡ x

f x 2 - g x 2 = 4   s e n   x cos ⁡ x = 2   s e n   2 x

Passo 2

Vamos calcular primeiro a área:

A = ∫ 0 π / 2 2 cos ⁡ x   d x = 2 s e n   x 0 π / 2 = 2 ⋅ 1 - 0 = 2

Portanto,

x - = 1 2 ∫ 0 π / 2 2   x cos ⁡ x   d x = ∫ 0 π / 2 x cos ⁡ x   d x

y - = 1 2 ∫ 0 π / 2 1 2 ⋅ 2   s e n   2 x   d x = 1 2 ∫ 0 π / 2 s e n   2 x   d x

Passo 3

Para a coordenada x , vamos usar integração por partes:

∫ u   d v = u v - ∫ v   d u

Tomando u = x e d v = cos ⁡ x   d x , temos que d u = d x e v = s e n   x :

x - = ∫ 0 π / 2 x cos ⁡ x   d x = x   s e n   x 0 π / 2 - ∫ 0 π / 2 s e n   x   d x

Assim,

x - = π 2 - 0 + cos ⁡ x 0 π 2 = π 2 + 0 - 1 = π 2 - 1

Já para a coordenada y :

y - = 1 2 ∫ 0 π / 2 s e n   2 x   d x = - 1 4 cos ⁡ 2 x 0 π 2 = - 1 4 cos ⁡ π - cos ⁡ 0 = 1 2

Portanto, as coordenadas do centroide serão:

π 2 - 1 , 1 2

Resposta

π 2 - 1 , 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

37- Determine o centro de massa de uma placa fina e plana que abrange a região compreendida pela parábola y 2 = x e pela reta x = 2 y , se a função densidade for δ y = 1 + y . (Use faixas horizontais.
Determine o centro de massa da região A dada.A = { ( x , y ) ∈ R 2 x 2 + 4 y 2 ≤ 1 ,y ≥ 0 }
Determine o centro de massa da região A dada A = { ( x , y ) ∈ R 2 x 2 ≤ y ≤ x }
Determine o centro de massa do gráfico da função dada. f x = 4 - x 2 ,- 2 ≤ x ≤ 2
Determine o centro de massa da função dada: f x = e x + e - x 2 ,- 1 ≤ x ≤ 1