Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.1 - Ex. 57
Use o gráfico da sequência para decidir quando a sequência é convergente ou divergente. Se a sequência é convergente, estime o valor do limite a partir do gráfico e, então, prove seu palpite. (Veja na nota de rodapé na página 699 para conselhos de gráficos de sequências.)
Passo 1
Beleza, galera? Vamos resolver essa questão de sequências.
Basicamente, o que precisamos fazer aqui é plotar o gráfico da nossa sequência e analisar para onde os valores dela vão se aproximando. Caso se aproximem de um valor fixo dizemos que essa sequência converge para certo valor e analisando a curva vamos conjecturar que valor seria esse.
Depois, para provar nosso palpite, é só calcular o limite de e ver se faz sentido com nosso palpite inicial.
Galerinha, uma sequência tem limite se conseguirmos fazer os termos de chegarem mais próximos de usando um valor para suficientemente grande. Se esse limite existe, podemos dizer que a sequência converge. Caso contrário, a sequência diverge.
Ah, e sobre a nota de rodapé na página 699, ela basicamente traz uma dica de como alguns sistemas de álgebra computacional nos permitem criar sequências e graficá-las diretamente. No entanto, com a maioria das calculadoras gráficas, as sequências podem ser graficadas utilizando equações paramétricas.
No nosso caso, usaremos o software GeoGebra, que já nos traz o gráfico diretamente quando utilizamos a função sequências.
Passo 2
Os primeiros termos da nossa sequência são:
Para
Para
Para
Para
Para :
Usando o software para plotar os pontos dessa sequência, temos:
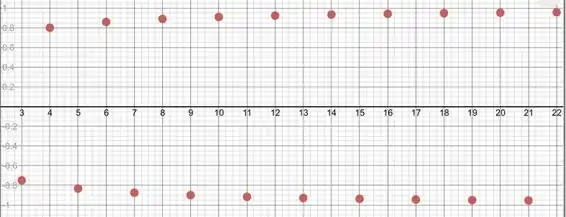
Do gráfico, parece que a sequência é divergente, não é? Até porque ela oscila entre e , aproximadamente.
Passo 3
Perceba só olhando pelo gráfico que não faz sentido falarmos em limite dessa sequência:
O termo é negativo para valores ímpares de e positivos para valores pares.
Dessa forma essa nossa sequência nunca terá um limite, ou seja, nunca se aproximará cada vez mais de um número fixo. Assim podemos dizer que a sequência diverge.
Resposta
A sequência diverge!