Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.3 - Ex. 54
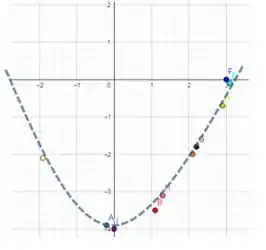
Use os gráficos dados de e para estimar o valor de para Use essas estimativas para esboçar o gráfico de .
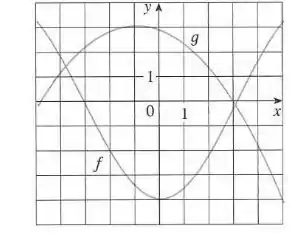
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos deu o gráfico das funções e e pediu pra gente descobrir o valor aproximado da composição , quando vai de até 5. Depois temos que montar um gráfico com esses resultados.
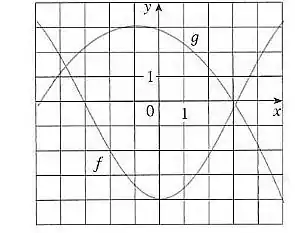
Observe que o exercício nos pede uma estimativa porque não conseguimos saber o valor exato desses pontos pelo gráfico, já não temos marcações tão específicas. Então, vamos sempre tentar encontrar primeiro o valor da função mais interna, que nesse caso é . Obtendo esse valor, vamos poder estimar o valor de nesse ponto e teremos o valor da composição .
Vamos lá!
Passo 2
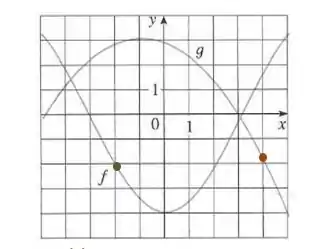
Vamos primeiro encontrar os valores de , observando o gráfico.
Assim, para , vamos ter o ponto:
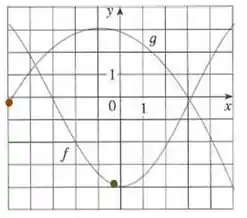
Logo,
Agora, vamos colocar esse resultado em , para fazer a composição que queremos. Observando o valor de em , temos:
Sendo assim, vamos dizer que o nosso primeiro ponto é . Esse vai ser um ponto que pertence à função de , e vai ser importante para montar o gráfico no nosso último passo.
Agora para , temos:
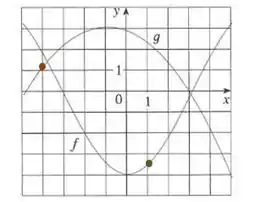
Logo,
Agora, colocando esse resultado em , encontramos:
Vamos dizer, então, que , outro ponto da
Legal, né? 😉
Para , temos o ponto em laranja:
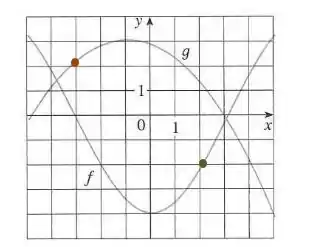
Logo,
Agora, colocando esse resultado em , para fazer a composição que queremos, obtemos:
Vamos criar, então, o ponto da função
Passo 3
Para , vamos ter:
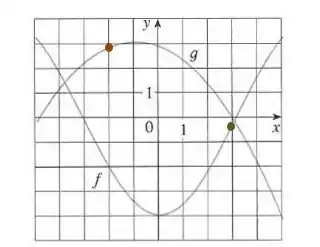
Logo,
Agora, colocando esse resultado em , para fazer a composição que queremos, observando o ponto em verde, temos:
E podemos criar o ponto da função
Vamos continuar...
Para , temos:
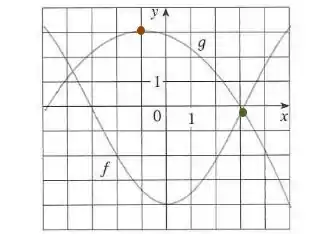
Logo,
Agora, colocando esse resultado em , para fazer a composição que queremos:
Vamos criar o ponto da função
Para , temos o ponto em laranja no eixo :
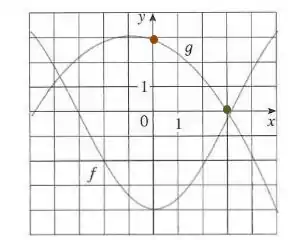
Isso nos dá:
Agora, colocando esse resultado em , para fazer a composição, temos:
Vamos criar o ponto da função
Estamos quase lá! 😇
Passo 4
Para , temos:
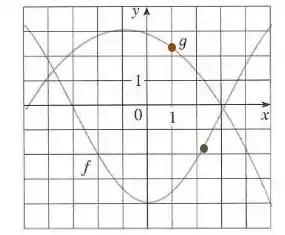
Então, nosso ponto será:
Agora, colocando esse resultado em , para fazer a composição das funções, obtemos no gráfico:
Vamos criar o ponto da função
Relaxa, estamos acabando!
Para , temos:
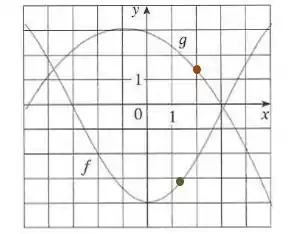
Logo,
Agora, colocando esse resultado em , para fazer a composição que queremos:
Vamos criar o ponto da função
Para , temos o ponto em laranja:
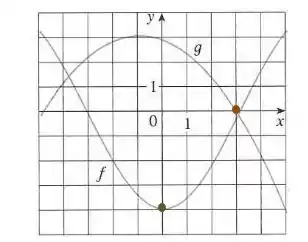
Sendo assim, ficamos com:
Agora, colocando esse resultado em , obtemos do gráfico:
Vamos criar o ponto da função
Passo 5
Para , temos:
Logo,
Agora, colocando esse resultado em , para fazer a composição que queremos:
Vamos criar o ponto da função
Aguenta aí! 😬
Passo 6
Para , temos o ponto laranja:
Logo,
Agora, colocando esse resultado em , para fazer a composição das funções, obtemos:
Vamos criar o ponto da função
Finamente!
Passo 7
Beleza, agora que já sabemos os valores estimados da função composta, vamos montar o gráfico com o auxílio do GeoGebra, colocando os pontos achados no plano cartesiano:
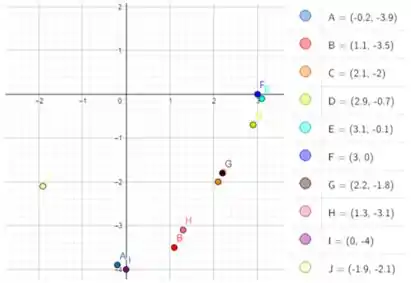
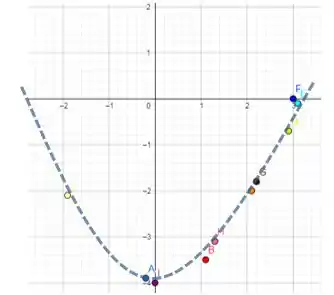
Agora, por último, só falta traçar o gráfico (aproximado) da função composta
Aqui vale lembrar que é apenas uma aproximação, já que não sabemos precisamente qual o valor de cada ou .
E aí! O que achou? Responde Aí! 😉
Resposta
