Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 2f
Use os gráficos dados para estimar o valor de cada derivada.
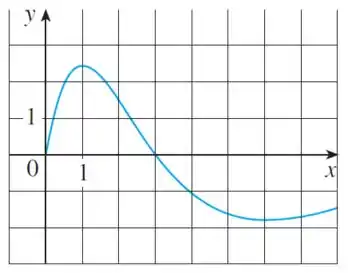
Passo 1
Opa, vamos fazer essa questão! O enunciado pede pra a gente estimar o valor de a partir do gráfico:
A derivada é uma taxa de variação do quanto varia em relação a em um intervalo muuuito pequenininho de que tende a zero! Ela pode ser calculada como sendo o coeficiente angular da reta tangente em determinado ponto, nesse caso .
Não vamos conseguir calcular precisamente, mas podemos desenhar a reta tangente e estimar sua inclinação! Bora lá?
Passo 2
Vamos então desenhar:
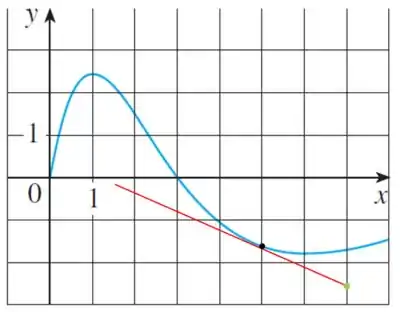
O nosso ponto ta representado de preto, temos a reta tangente em vermelho e em verde temos um segundo ponto que pertence a reta tangente. Dessa forma podemos calcular o coeficiente angular da reta, fazendo:
Podemos estimar como e como . Calculando:
Podemos então estimar que: