Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.Exercícios Práticos - Ex. 122
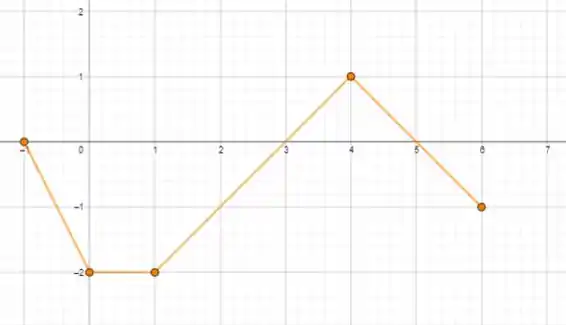
Use as informações a seguir para fazer o gráfico da função para
O gráfico de é formado por segumentos de reta unidos pelas extremidades
o gráfico tem início no ponto
A derivada de , onde é definida, correponde à função escada mostrada aqui:
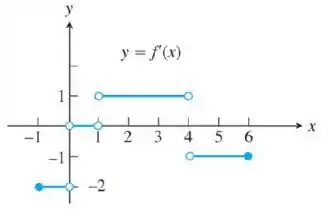
Passo 1
Primeiramente, vamos entender como é sse gráfico. Ele disse o enunciado que são diversos segmentos de reta certo? O que vamos ter é uma reta que começa em e vai mudando sua inclinação de acordo com o gráfico que ele deu.
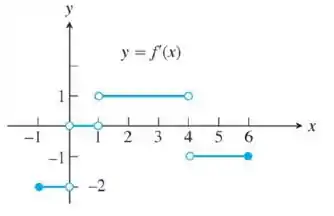
Então teremos uma equação de a , depois de a , de a e pot fim de a
Vamos escrever cada intervalo desse separadamente.
Passo 2
Começando com
A equação da reta é
A derivada dela vai ser
Pelo gráfico da derivada, teremos:
E a equação da reta fica:
Dessa forma, usando o ponto , vamos ter
A reta fica:
E ela vai terminar no ponto onde , que vai ser:
ou seja, no ponto
Passo 3
Agora para com
A equação da reta é
A derivada dela vai ser
Pelo gráfico da derivada, teremos:
E a equação da reta fica:
A reta vai começar onde a anterior terminou, em , destsa forma vamos ter:
A reta fica:
E ela vai terminar no ponto onde , que vai ser:
ou seja, no ponto
Passo 4
Agora para com
A equação da reta é
A derivada dela vai ser
Pelo gráfico da derivada, teremos:
E a equação da reta fica:
A reta vai começar onde a anterior terminou, em , destsa forma vamos ter:
A reta fica:
E ela vai terminar no ponto onde , que vai ser:
ou seja, no ponto
Passo 5
Terminando com com
A equação da reta é
A derivada dela vai ser
Pelo gráfico da derivada, teremos:
E a equação da reta fica:
A reta vai começar onde a anterior terminou, em , destsa forma vamos ter:
A reta fica:
E ela vai terminar no ponto onde , que vai ser:
ou seja, no ponto
Passo 6
A nossa função vai ficar:
O gráfico vai ser retas que ligam os pontos na seguinte ordem:
O gráfico vai ficar:
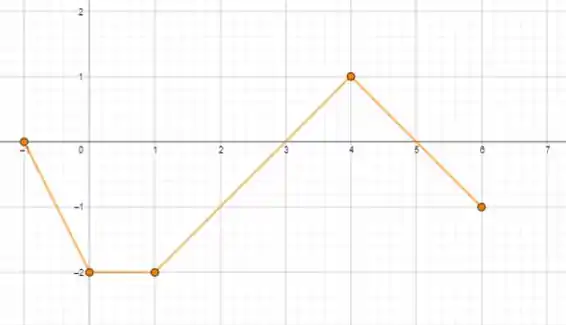
Resposta
