Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.1 - Ex. 72
a) Use a integração por partes para mostrar que
b) Se e são funções inversas e é contínua, demonstre que
[Sugestão: Use a parte (a) e faça a substituição ]
c) No caso em que e são funções positivas e , desenhe um diagrama para dar uma interpretação geométrica à parte (b).
d) Use a parte (b) para calcular
Passo 1
E aí! Suave? 😉
Nesse problema queremos mostrar que pelo método de integração por partes e se e forem funções inversas e for contínua, então .
Muita coisa, né? 👀
O método de integração por partes é uma técnica para calcular integrais que envolvem o produto de duas funções. Esse método se baseia na regra do produto para a derivada, que diz que:
Integrando ambos os membros dessa igualdade, obtemos:
Isolando a integral que queremos calcular, temos:
Veja só! 😉
Passo 2
Se fizermos e , temos que e
Ou seja, pelo que vimos no passo 1, temos
Para provar que
Usaremos , de modo que e
Então,
Tranquilo até aqui? 😬
Passo 3
A parte (b) diz que a área da região é
Assim, temos o seguinte diagrama:
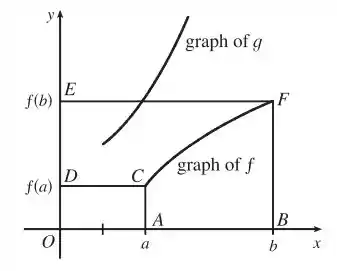
Legal, né? 😊
Passo 4
Nós temos que , então, , e desde que , nós temos que .
Pela parte (b), conseguimos chegar na seguinte integral:
Calculando a integral e aplicando os limites de integração
E aí! Entendeu tudo? Responde Aí! 😉
Resposta
Respostas nos passos!