Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.7 - Ex. 22

  1. Na Regra do Ponto médio para as Integrais Triplas usamos a soma tripla de Riemann para aproximar a integral tripla sobre uma caixa B, onde f ( x , y , z ) é calculada no centro ( x - , y - , z - ) da caixa B i j k . Utilize a Regra do Ponto Médio para estimar ∭ B e - x 2 - y 2 - z 2 d V , onde B é o cubo definido po 0 ≤ x ≤ 1 , 0 ≤ y ≤ 1 , 0 ≤ z ≤ 1 . Divida B em oito cubos de tamanho igual.
  2. Use um sistema de computação algébrica para aproximar a integral da parte (a) com a precisão até duas casas decimais. Compare com a resposta da parte (a).

Passo 1

Vamos lá meu amigo! Vamos entender essa questão, queremos utilizar a regra do ponto médio para integrais Triplas usando a soma tripla de Riemann para estimar a seguinte integral:

∭ B e - x 2 - y 2 - z 2 d V

Sendo B um cubo de 0 a 1 em todas as direções. O exercício quer que esse cubo seja separado em 8 partes. Depois disso, precisaremos utilizar computação algébricaa para obter um resultado aproximada.

Vamos entender o que é essa regra do ponto médio? Bem , temos que uma integral tripla pode ser definida da seguinte forma:

∭ B f x , y , z d V = lim l , m , n → ∞ ⁡ ∑ i l ∑ j m ∑ k n f x i j k * , y i j k * , z i j k * ∆ V

De forma simplificada, iremos calcular o valor de ∆ V e multiplicar pela função para cada valor de x , y e z , definido pelas subdivisões do cubo B em 8 partes. Veja:

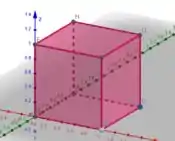
Se quisermos dividir esse cubo em 8 teremos que dividir cada arestar pela metade:

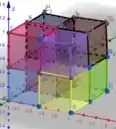
Porém, iremos utilizar regra do ponto médio, isso significa que iremos utilizar o ponto médio de cada uma das arestas desses cubos como, ou seja: Os pontos 1 4 , 3 4 nos eixos x , y e z .

Passo 2

  1. Precisamos calcular ∆ V que é o volume de cada cubo criado na subdivisão. Ou seja:

    2. ∆ V = 1 2 3 = 1 8

    Então a Regra do Ponto Médio nos dá que:

    ∭ B e - x 2 - y 2 - z 2 d V = lim l , m , n → ∞ ⁡ ∑ 1 l ∑ 1 m ∑ 1 n e - x 2 - y 2 - z 2 ∆ V

    Abrindo os somatórios teremos:

    1 8 f 1 4 , 1 4 , 1 4 + f 1 4 , 1 4 , 3 4 + f 1 4 , 3 4 , 1 4 + f 3 4 , 1 4 , 1 4 + f 3 4 , 1 4 , 3 4 + f 3 4 , 1 4 , 3 4

    + f 3 4 , 3 4 , 1 4 + f 3 4 , 3 4 , 3 4  

    Utilizando f x , y , z =   e - x 2 - y 2 - z 2

    = 1 8 e - 3 1 / 4 2 + 3 e - 2 1 / 4 2 - 3 / 4 2 + 3 e - 1 / 4 2 - 2 3 / 4 2 + e - 3 3 / 4 2 ≈ 0.42968          

    Passo 2

  2. Um CAS estima a integral a ser ∭ B e - x 2 - y 2 - z 2 d V ≈ 0,42

A estimativa na parte (a) está correta para uma casa decimal e é maior que o valor real da integral.

Resposta

  1. ≈ 0.42968    
  2. ≈ 0,42
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular o volume do sólido delimitado pelos planos y = 0 ,z = 0 ,x + y = 4 e pelo cilindro parabólico z = 1 - x 2 .
Calcular o volume do sólido acima do plano xy delimitado por z = x 2 + y 2 e x 2 + y 2 = 16 .
Calcular o volume do sólido acima do paraboloide z = x 2 + y 2 e abaixo do cone z = x 2 + y 2 .
Calcular o volume do sólido acima do plano xy e interior às superfícies z = 9 - x 2 - y 2 e x 2 + y 2 = 1 .
Calcular o volume do tetraedro delimitado pelos planos coordenados e pelo plano x a + y b + z c = 1 .