Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.4 - Ex. 6
Encontre a massa e o centro de massa da lamina que ocupa a região e é dada pela função da densidade .
Passo 1
Fala, pessoal! Tudo bem?
A questão quer a massa e o centro de massa da lâmina com densidade:
Ocupando a região , onde:
é a região triangular limitada pelas linhas
Para encontrar a massa da lâmina aplicamos a integral:
E para o centro de massa precisamos achar o valor de:
E:
Então, nosso objetivo é calcular essas 3 integrais, primeiro calculando seus limites de integração, que vamos tirar da região .
Lembrando que:
Vamo lá!
Passo 2
Bom... Temos que encontrar a massa e o centro de massa da lâmina que ocupa a região quando a função densidade é . Mas nosso primeiro passo aqui deve ser encontrar quais limites de integração para e para vamos usar no cálculo das nossas integrais duplas. Vamos esboçar a região com as equações e dados que foram dados no enunciado:
é a região triangular limitada pelas linhas
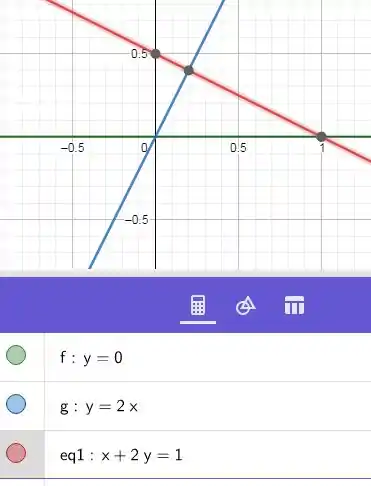
Podemos observar que as linhas formam a região triangular que delimita o nosso sistema.
A partir do gráfico fica claro que os dois vértices são e . O terceiro vértice não dá pra gente obter só olhando o gráfico com precisão, então vamos igualas as linhas (azul) e (vermelha), porque assim a gente acha o ponto de intersecção entre as duas.
Vamos lá:
Começando, temos:
Vamos multiplicar por essa equação:
Agora substituindo na equação da outra reta:
Ficamos com:
Que nos dá:
Para achar , substituímos o valor de que achamos em uma das retas:
Assim, o terceiro vértice é dado por .
Agora que sabemos os vértices podemos limitar a nossa integral e assim ter os limites de integração.
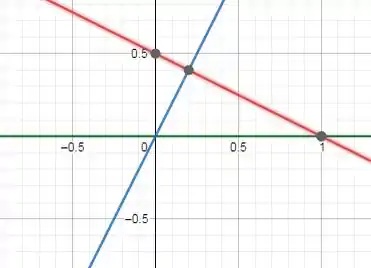
Observando novamente a figura podemos dizer que varia entre duas constantes ( e ) e varia entre duas funções: reta e vai até .
Passo 3
A massa da lâmina é dada por:
A nossa integral vai ser:
Perceba que colocar “por dentro” a integral que tem incógnitas nos seus limites de integração. Resolvendo primeiro a integral de dentro temos:
Aplicando os limites de integração:
Simplificando os termos:
Substituindo na integral de fora, temos:
Resolvendo, temos:
Aplicando os limites de integração:
Portanto a massa da lâmina é:
Passo 4
O centro de massa da lâmina que ocupa a região e que possui função de densidade é:
Resolvendo , temos:
Fazendo a divisão de frações na constante para fora da integral:
Resolvendo a integral de dentro:
Aplicando os limites de integração:
Simplificando as frações:
Agora a integral de fora:
Aplicando os limites de integração:
Nossa coordenada do centro de massa é:
Passo 5
Vamos fazer o mesmo para encontrar , resolver:
Fazendo a divisão de frações na constante para fora da integral:
Resolvendo a integral de dentro:
Aplicando os limites de integração:
Simplificando as frações:
Agora a integral de fora:
Aplicando os limites de integração:
Portanto, nosso da coordenada do centro de massa é:
Portanto o centro de massa é o ponto: