Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 6.3 - Ex. 6
Use o método das cascas cilíndricas para achar o volume gerado pela rotação em torno do eixo da região limitada pelas curvas dadas. Esboce a região e uma casca típica.
Passo 1
Fala aí! como vai?
Nesse problema temos que usar o método das cascas cilíndricas para obter o volume do solido gerado pela rotação das curvas
Ao redor do eixo .
Parece complicado?
O método das cascas cilíndricas é calculado quando a rotação é feita no eixo pela equação
Veja só!
Passo 2
Esboçando a região e uma casca típica:
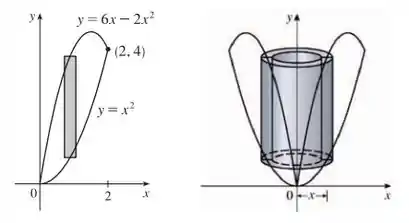
Bora lá!
Passo 3
Igualando as funções para encontrar onde elas se tocam, logo, o limite da casca temos
Calculando o volume:
Substituindo os valores
Calculando a integral e aplicando os limites de integração...
E aí! o que achou? Responde Aí!
Resposta
.
Exercícios de Livros Relacionados
Use o método das cascas cilíndricas para encontrar o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno do eixo x . Esboce a região e uma casca típica. x = y ,x = 0
Escreva, mas não calcule, uma integral para o volume de um sólido obtido pela rotação da região limitada pelas curvas dadas em torno do eixo especificado. y = x ,y = 4 x - x ² ; ² em torno de x = 7
Use o método das cascas cilíndricas para encontrar o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno do eixo x . Esboce a região e uma casca típica. x = 4 y 2 - y
Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região delimitada pelas curvas dadas em torno do eixo especificado. Esboce a região e uma casca típica. y = x 2 ,y = 2 -
Escreva, mas não calcule, uma integral para o volume de um sólido obtido pela rotação da região limitada pelas curvas dadas em torno do eixo especificado. y = x 4 ,y = sen π x 2 ; em torno de x = -