Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.3 - Ex. 12
Use o método das cascas cilíndricas para encontrar o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno do eixo . Esboce a região e uma casca típica.
Passo 1
Nós temos os seguintes esboços, da região e casca típica:
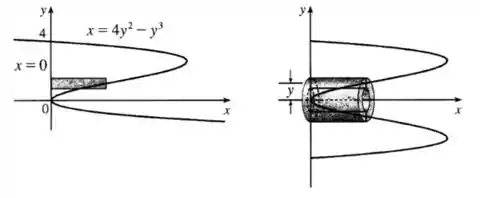
Passo 2
Podemos ver que a função varia de a em da seguinte forma:
Assim, temos o seguinte cálculo:
Resposta
.
Exercícios de Livros Relacionados
Ache o volume do sólido gerado pela rotação, em torno do eixo y, da região limitada pelo gráfico de y = 4 x - 1 8 x 4 , pelo eixo x e pela reta x = 2 .
Nos exercícios de 21 a 24, a região é limitada pelas curvas x = y 2 - 2ex = 6 - y 2 gira em torno do eixo indicado. Ache o volume do sólido gerado.23.a reta x = 2
Ache o volume do sólido gerado pela rotação da região limitada pelas curvas y = x 3 e x = y 3 em torno do eixo x. Tome os elementos retangulares de área paralelos ao eixo de revolução.
Ache o volume do sólido gerado pela rotação da região limitada pela curva y = s e n ( x 2 ) , pelo eixo x e pelas retas x = 1 2 π e x = π em torno do eixo y.
Ache o volume do sólido gerado pela rotação da região limitada por aquela reta e pela parábola x 2 = 4 y em torno da reta y = 1 . Tome os elementos retangulares de área paralelos ao eixo de revolução.