Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.4 - Ex. 37

Use o método desta secção para encontrar a área de um trapézio isósceles cujas bases têm medidas b 1 e b 2 e cuja altura tem medida h .

Passo 1

Abaixo nós temos o esboço de um trapézio isósceles e vamos usar o método de somar áreas de reângulos para achar a área total.

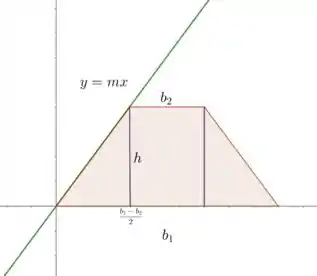
Observe que um trapézio isósceles pode ser dividido em um retângulo e dois triângulos iguais. Sendo assim a área do trapézio será:

Á r e a = 2 ⋅ A 1 + A 2

Sendo A 1 a área do triângulo e A 2 do retângulo.

Passo 2

Vamos começar calculando A 1 e para isso vamos descobrir quem é m da reta m x . Como m é o coeficiente angular da reta, podemos fazer a tangente do triângulo retângulo de catetos h e b 1 - b 2 2 .

m = tan ⁡ θ = h b 1 - b 2 2 = 2 h b 1 - b 2

Dessa forma, y = 2 h b 1 - b 2 x .

Para calcular a área da região abaixo de y = m x , em um intervalo [ a , b ] com   a > b > 0 , fazemos o seguinte:

Δ x = b - a n

f x i = m a + i b - a n

A = lim n → + ∞ ⁡ ∑ i = 1 n f ( x i ) Δ x = lim n → + ∞ ⁡ ∑ i = 1 n m a + i b - a n b - a n  

Agora vamos usar as fórmulas dos somatórios e calcular o limite.

∑ i = 1 n 1 ⏞ I = n                                 ∑ i = 1 n i ⏞ = I I n ( n + 1 ) 2

A = lim n → + ∞ ⁡ m b - a n a n + b - a n ⋅ n ( n + 1 ) 2

A = lim n → + ∞ m ⁡ b - a n a n + b - a 2 n + 1

A = lim n → + ∞ m ⁡ ( b - a ) a n n + b - a 2 1 + 1 n

A = m ⁡ ( b - a ) a + b - a 2 1 + 0

A = m ⁡ ( b - a ) 2 a + b - a 2

A = m ⁡ 2 a b - a + b - a 2 2

A = m ⁡ 2 a b - 2 a 2 + b 2 - 2 a b + a 2 2

A = m ⁡ - 2 a 2 + b 2 + a 2 2

A = m ⁡ b 2 - a 2 2     u . a

Logo, a área A é m ⁡ b 2 - a 2 2     u . a .

Só que nosso intervalo será 0 , b 1 - b 2 2 , ou seja, a = 0 e b = b 1 - b 2 2 e também sabemos que m = 2 h b 1 - b 2 . Sendo assim

A 1 = 2 h b 1 - b 2 ⁡ b 1 - b 2 2 2 - 0 2 2 = 2 h b 1 - b 2 ⋅ b 1 - b 2 2 8 = h b 1 - b 2 4

A 1 = h b 1 - b 2 4   u . a

Passo 3

A 2 será a área do retângulo de base b 2 e altura h , ou seja, A 2 = b 2 ⋅ h

Passo 4

Agora juntamos tudo.

Á r e a = 2 ⋅ A 1 + A 2 = 2 h b 1 - b 2 4 + b 2 ⋅ h

Á r e a = h b 1 - b 2 2 + 2 b 2 ⋅ h 2 = h ( b 1 - b 2 + 2 b 2 ) 2 = h ( b 1 + b 2 ) 2

Logo, a área do trapézio será h ( b 1 + b 2 ) 2     u . a .

Resposta

A = h ( b 1 + b 2 ) 2 ⁡   u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse o limite como uma integral definida. lim n → ∞ ⁡ ∑ i = 1 n i 4 n 5 [Sugestão: Considere f x = x 4 .]
Expresse o limite como uma integral definida. lim n → ∞ ⁡ 1 n ∑ i = 1 n 1 1 + i n 2
Seja f x = 0 se x for um número racional qualquer e f x = 1 se x for um número irracional qualquer. Mostre que f não é integrável em 0,1 .
Seja f 0 = 0 e f x = 1 x se 0x ≤ 1 . Mostre que f não é integrável em 0,1 . [Sugestão: mostre que o primeiro termo na soma de Riemann, f x i * Δ x , pode ser tornado arbitrariamente grande.]
Encontre ∫ 1 2 x - 2 d x . Sugestão: Escolha x i * como a média geométrica de x i - 1 e x i (isto é, x i * = x i - 1 x i ) e use a identidade 1 m m + 1 = 1 m - 1 m + 1